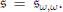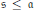Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
GUZMÁN-GONZÁLEZ, OSVALDO
HRUŠÁK, MICHAEL
MARTÍNEZ-RANERO, CARLOS AZAREL
and
RAMOS-GARCÍA, ULISES ARIET
2017.
GENERIC EXISTENCE OF MAD FAMILIES.
The Journal of Symbolic Logic,
Vol. 82,
Issue. 1,
p.
303.
Guzmán, Osvaldo
2019.
There is a +-Ramsey MAD family.
Israel Journal of Mathematics,
Vol. 229,
Issue. 1,
p.
393.
Corral, César
and
Hrušák, Michael
2020.
Fréchet-like properties and almost disjoint families.
Topology and its Applications,
Vol. 277,
Issue. ,
p.
107216.
Corral, C.
2021.
Madness and weak forms of normality.
Acta Mathematica Hungarica,
Vol. 165,
Issue. 2,
p.
291.
FERREIRA, SALVADOR GARCÍA
and
GUZMÁN, OSVALDO
2022.
MORE ON FRÉCHET–URYSOHN IDEALS.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
829.
GUZMÁN, OSVALDO
2024.
KATĚTOV ORDER ON MAD FAMILIES.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
794.