Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Huanyin
and
Sheibani, Marjan
2017.
Strongly 2-nil-clean rings.
Journal of Algebra and Its Applications,
Vol. 16,
Issue. 09,
p.
1750178.
Zhou, Yiqiang
2018.
Rings in which elements are sums of nilpotents, idempotents and tripotents.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 01,
p.
1850009.
Chen, Huanyin
and
Sheibani, Marjan
2018.
Structure of Zhou Nil-clean Rings.
Algebra Colloquium,
Vol. 25,
Issue. 03,
p.
361.
Danchev, Peter V.
2018.
Rings Whose Elements are Sums of Three or Differences of Two Commuting Idempotents.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 6,
p.
1641.
Abdolyousefi, Marjan Sheibani
and
Chen, Huanyin
2018.
Matrices over Zhou nil-clean rings.
Communications in Algebra,
Vol. 46,
Issue. 4,
p.
1527.
Danchev, Peter V.
2018.
RINGS WHOSE ELEMENTS ARE SUMS OF THREE OR MINUS SUMS OF TWO COMMUTING IDEMPOTENTS.
Albanian Journal of Mathematics,
Vol. 12,
Issue. 1,
Chen, H.
and
Sheibani, M.
2019.
Rings Whose Every Subring is Feebly Clean.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 1,
p.
257.
Abyzov, A. N.
2019.
Strongly q-Nil-Clean Rings.
Siberian Mathematical Journal,
Vol. 60,
Issue. 2,
p.
197.
Danchev, P. V.
2019.
Rings Whose Elements Are Linear Combinations of Three Commuting Idempotents.
Lobachevskii Journal of Mathematics,
Vol. 40,
Issue. 1,
p.
36.
Abdolyousefi, Marjan Sheibani
Ashrafi, Nahid
and
Chen, Huanyin
2019.
On Unit Nil-Clean Rings.
Mediterranean Journal of Mathematics,
Vol. 16,
Issue. 4,
Tang, Gaohua
Zhou, Yiqiang
and
Su, Huadong
2019.
Matrices over a commutative ring as sums of three idempotents or three involutions.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 2,
p.
267.
Cui, Jian
and
Yin, Xiaobin
2020.
Rings with 2-UJ property.
Communications in Algebra,
Vol. 48,
Issue. 4,
p.
1382.
PETİK, Tuğba
HOCAOĞLU, Leman
and
ÖZDEMİR, Halim
2020.
Üçgensel Matris Halkalarında İnvolutifler.
Bilecik Şeyh Edebali Üniversitesi Fen Bilimleri Dergisi,
Vol. 7,
Issue. 1,
p.
91.
Cui, Jian
and
Danchev, Peter
2020.
Some new characterizations of periodic rings.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 12,
p.
2050235.
Abyzov, A. N.
and
Tapkin, D. T.
2021.
Rings over Which Matrices Are Sums of Idempotent and $ q $-Potent Matrices.
Siberian Mathematical Journal,
Vol. 62,
Issue. 1,
p.
1.
Aristidou, Michael
and
Hailemariam, Kidus
2021.
Tripotent elements in quaternion rings over ℤp
.
Acta Universitatis Sapientiae, Mathematica,
Vol. 13,
Issue. 1,
p.
78.
Xia, Guoli
Tang, Gaohua
and
Zhou, Yiqiang
2021.
When is a matrix a sum of involutions or tripotents?.
Communications in Algebra,
Vol. 49,
Issue. 4,
p.
1717.
Abyzov, A.N.
and
Tapkin, D.T.
2021.
When is every matrix over a ring the sum of two tripotents?.
Linear Algebra and its Applications,
Vol. 630,
Issue. ,
p.
316.
Abyzov, A. N.
and
Tapkin, D. T.
2022.
On rings with xn − x nilpotent.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 06,
Ma, Guanglin
and
Wang, Yao
2022.
On weak zero-clean rings.
International Journal of Algebra and Computation,
Vol. 32,
Issue. 08,
p.
1459.
 $R$ be a ring. The following results are proved.
$R$ be a ring. The following results are proved. 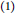 $\left( 1 \right)$ Every element of
$\left( 1 \right)$ Every element of  $R$ is a sum of an idempotent and a tripotent that commute if and only if
$R$ is a sum of an idempotent and a tripotent that commute if and only if  $R$ has the identity
$R$ has the identity 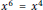 ${{x}^{6}}\,=\,{{x}^{4}}$ if and only if
${{x}^{6}}\,=\,{{x}^{4}}$ if and only if 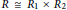 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where 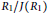 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 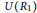 $U\left( {{R}_{1}} \right)$ a group of exponent
$U\left( {{R}_{1}} \right)$ a group of exponent  $2$ and
$2$ and 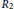 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 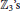 ${{\mathbb{Z}}_{3}}^{,}s$.
${{\mathbb{Z}}_{3}}^{,}s$. 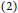 $\left( 2 \right)$ Every element of
$\left( 2 \right)$ Every element of  $R$ is either a sum or a difference of two commuting idempotents if and only if
$R$ is either a sum or a difference of two commuting idempotents if and only if 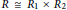 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}$, where 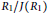 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 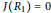 $J\left( R \right)\,=\,0$ or
$J\left( R \right)\,=\,0$ or 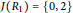 $J\left( R \right)\,=\,\left\{ 0,\,2 \right\}$ and
$J\left( R \right)\,=\,\left\{ 0,\,2 \right\}$ and 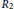 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 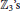 ${{\mathbb{Z}}_{3}}^{,}s$.
${{\mathbb{Z}}_{3}}^{,}s$. 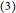 $\left( 3 \right)$ Every element of
$\left( 3 \right)$ Every element of  $R$ is a sum of two commuting tripotents if and only if
$R$ is a sum of two commuting tripotents if and only if 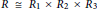 $R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}\,\times \,{{R}_{3}}$, where
$R\,\cong \,{{R}_{1}}\,\times \,{{R}_{2}}\,\times \,{{R}_{3}}$, where 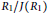 ${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with
${{{R}_{1}}}/{J\left( {{R}_{1}} \right)}\;$ is Boolean with 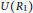 $U\left( {{R}_{1}} \right)$ a group of exponent
$U\left( {{R}_{1}} \right)$ a group of exponent  $2$
,
$2$
, 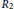 ${{R}_{2}}$ is zero or a subdirect product of
${{R}_{2}}$ is zero or a subdirect product of 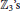 ${{\mathbb{Z}}_{3}}^{,}s$, and
${{\mathbb{Z}}_{3}}^{,}s$, and 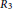 ${{R}_{3}}$ is zero or a subdirect product of
${{R}_{3}}$ is zero or a subdirect product of 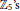 ${{\mathbb{Z}}_{5}}^{,}s$.
${{\mathbb{Z}}_{5}}^{,}s$.



