Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-23T10:36:29.832Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Discriminants of the Powers of an Algebraic Integer

Part of: Diophantine approximation, transcendental number theory Algebraic number theory: global fields

Published online by Cambridge University Press:  22 May 2019

Stéphane R. Louboutin
Stéphane R. Louboutin*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, I2M, Marseille, France Email: stephane.louboutin@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

For $\unicode[STIX]{x1D6FC}$ an algebraic integer of any degree 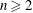$n\geqslant 2$, it is known that the discriminants of the orders 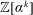$\mathbb{Z}[\unicode[STIX]{x1D6FC}^{k}]$ go to infinity as 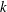$k$ goes to infinity. We give a short proof of this result.

Keywords

discriminantalgebraic integer

MSC classification

Primary: 11R04: Algebraic numbers; rings of algebraic integers
Secondary: 11R29: Class numbers, class groups, discriminants 11J86: Linear forms in logarithms; Baker's method
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 481 - 483
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dubickas, A., On the discriminant of the power of an algebraic number. Stud. Sci. Math. Hungar. 44(2007), 27–34. https://doi.org/10.1556/SScMath.2006.1001Google Scholar
Evertse, J.-H. and Györy, K., Discriminant equations in Diophantine number theory. New Math. Monogr., 32, Cambridge University Press, Cambridge, 2017. https://doi.org/10.1017/CBO9781316160763CrossRefGoogle Scholar
Grossman, E. H., Units and discriminants of algebraic number fields. Comm. Pure Appl. Math. 27(1974), 741–747. https://doi.org/10.1002/cpa.3160270603CrossRefGoogle Scholar
Louboutin, S., On some cubic or quartic algebraic units. J. Number Theory 130(2010), 956–960. https://doi.org/10.1016/j.jnt.2009.09.002CrossRefGoogle Scholar
Louboutin, S., On the fundamental units of a totally real cubic order generated by a unit. Proc. Amer. Math. Soc. 140(2012), 429–436. https://doi.org/10.1090/S0002-9939-2011-10924-9CrossRefGoogle Scholar
Louboutin, S., Fundamental units for some orders generated by a unit. In: Publ. Math. Besançon Algèbre et Théorie des Nombres, Presses Univ. Franche-Comté, Besançon, 2015, pp. 41–68.Google Scholar