Article contents
On a Yamabe Type Problem in Finsler Geometry
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper, a newnotion of scalar curvature for a Finsler metric  $F$ is introduced, and two conformal invariants
$F$ is introduced, and two conformal invariants 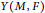 $Y(M,F)$ and
$Y(M,F)$ and 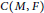 $C(M,F)$ are defined. We prove that there exists a Finsler metric with constant scalar curvature in the conformal class of
$C(M,F)$ are defined. We prove that there exists a Finsler metric with constant scalar curvature in the conformal class of  $F$ if the Cartan torsion of
$F$ if the Cartan torsion of  $F$ is sufficiently small and
$F$ is sufficiently small and 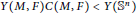 $Y(M,F)C(M,F)<Y({{\mathbb{S}}^{n}})$ where
$Y(M,F)C(M,F)<Y({{\mathbb{S}}^{n}})$ where 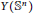 $Y({{\mathbb{S}}^{n}})$ is the Yamabe constant of the standard sphere.
$Y({{\mathbb{S}}^{n}})$ is the Yamabe constant of the standard sphere.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 3
- Cited by




