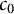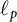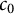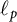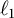1 Introduction
Let
![]() $(X,\|\cdot \|)$
be a Banach space with dual space
$(X,\|\cdot \|)$
be a Banach space with dual space
![]() $(X^*,\|\cdot \|_{*})$
, let
$(X^*,\|\cdot \|_{*})$
, let
![]() $(e_i)$
be a semi-normalized basic sequence in X, and let
$(e_i)$
be a semi-normalized basic sequence in X, and let
![]() $\alpha = \sum _{i=1}^n a_i e_i$
and
$\alpha = \sum _{i=1}^n a_i e_i$
and
![]() $\beta = \sum _{i=1}^m b_i e_i$
, where
$\beta = \sum _{i=1}^m b_i e_i$
, where
![]() $b_m \ne 0$
, belong to
$b_m \ne 0$
, belong to
![]() $\operatorname {span}((e_i))$
. Define
$\operatorname {span}((e_i))$
. Define
 $$ \begin{align} \alpha \otimes \beta = \sum_{i=1}^n a_i\bigg(\sum_{j=1}^m b_j e_{(i-1)m+j}\bigg)\end{align} $$
$$ \begin{align} \alpha \otimes \beta = \sum_{i=1}^n a_i\bigg(\sum_{j=1}^m b_j e_{(i-1)m+j}\bigg)\end{align} $$
and
![]() $\alpha \otimes 0 = 0$
. Note that
$\alpha \otimes 0 = 0$
. Note that
![]() $(\operatorname {span}((e_i)),\otimes )$
is a noncommutative semigroup with identity element
$(\operatorname {span}((e_i)),\otimes )$
is a noncommutative semigroup with identity element
![]() $e_1$
. However, the semigroup multiplication is not continuous.
$e_1$
. However, the semigroup multiplication is not continuous.
If
![]() $(e_i)$
is equivalent to the unit vector basis (u.v.b.) of
$(e_i)$
is equivalent to the unit vector basis (u.v.b.) of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
(
$\ell _p$
(
![]() $1 \le p < \infty $
), then there exists
$1 \le p < \infty $
), then there exists
![]() $K>0$
such that for all
$K>0$
such that for all
![]() $\alpha , \beta \in \operatorname {span}((e_i))$
,
$\alpha , \beta \in \operatorname {span}((e_i))$
,
The following is the main open question related to this note.
Question 1.1 Let
![]() $(e_i)$
be a semi-normalized basis for X satisfying (1.2). Is
$(e_i)$
be a semi-normalized basis for X satisfying (1.2). Is
![]() $(e_i)$
equivalent to the u.v.b. of
$(e_i)$
equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
for some
$\ell _p$
for some
![]() $1 \le p < \infty $
?
$1 \le p < \infty $
?
We prove below that Question 1.1 has a positive answer when
![]() $(e_i)$
is either bidemocratic, almost greedy, or invariant under spreading. However, we do not know the answer in general or for other natural classes of bases such as the class of unconditional bases.
$(e_i)$
is either bidemocratic, almost greedy, or invariant under spreading. However, we do not know the answer in general or for other natural classes of bases such as the class of unconditional bases.
Suppose that
![]() $(e_i)$
is a symmetric basis for X and that both X and
$(e_i)$
is a symmetric basis for X and that both X and
![]() $[(e^*_i)]$
have a unique symmetric basic sequence up to equivalence. Altshuler [Reference Altshuler3] proved that
$[(e^*_i)]$
have a unique symmetric basic sequence up to equivalence. Altshuler [Reference Altshuler3] proved that
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
. This theorem was recently extended to subsymmetric bases [Reference Casazza, Dilworth, Kutzarova and Motakis6]. In Section 3, we adapt Altshuler’s proof to give an answer to Question 1.1 for bidemocratic bases (see Section 2 for the definition of democratic and bidemocratic bases) by imposing on
$\ell _p$
. This theorem was recently extended to subsymmetric bases [Reference Casazza, Dilworth, Kutzarova and Motakis6]. In Section 3, we adapt Altshuler’s proof to give an answer to Question 1.1 for bidemocratic bases (see Section 2 for the definition of democratic and bidemocratic bases) by imposing on
![]() $(e_i)$
a condition that is formally weaker than (1.2). In Section 4, we provide a new characterization of
$(e_i)$
a condition that is formally weaker than (1.2). In Section 4, we provide a new characterization of
![]() $\ell _1$
which implies a solution to Question 1.1 under additional assumptions. The proof uses Szemerédi’s theorem on arithmetic progressions. In Section 5, we use the latter characterization to provide an answer to Question 1.1 for the class of democratic bases.
$\ell _1$
which implies a solution to Question 1.1 under additional assumptions. The proof uses Szemerédi’s theorem on arithmetic progressions. In Section 5, we use the latter characterization to provide an answer to Question 1.1 for the class of democratic bases.
The final section contains results about subsequences. We prove that Question 1.1 has a positive solution if
![]() $(e_i)$
is invariant under spreading or, more generally, if every subsequence of
$(e_i)$
is invariant under spreading or, more generally, if every subsequence of
![]() $(e_i)$
satisfies (1.2). Using infinite Ramsey theory, we also prove a related characterization of basic sequences which are saturated by subsequences equivalent to the u.v.b. of
$(e_i)$
satisfies (1.2). Using infinite Ramsey theory, we also prove a related characterization of basic sequences which are saturated by subsequences equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
2 Notation and terminology
We use standard Banach space theory notation and terminology as in [Reference Lindenstrauss and Tzafriri13]. We also require some terminology and results from the theory of greedy bases which we briefly review here. For further information on this topic, we refer the reader to [Reference Albiac and Kalton2, Reference Temlyakov15].
Let
![]() $(e_i)$
be a semi-normalized basic sequence in X. For finite
$(e_i)$
be a semi-normalized basic sequence in X. For finite
![]() $A \subset \mathbb {N}$
, let
$A \subset \mathbb {N}$
, let
![]() $\lambda (A) = \|\sum _{i \in A} e_i\|$
. The fundamental function
$\lambda (A) = \|\sum _{i \in A} e_i\|$
. The fundamental function
![]() $(\Phi (n))$
of
$(\Phi (n))$
of
![]() $(e_i)$
is defined by
$(e_i)$
is defined by
We say that
![]() $(e_i)$
is democratic with constant
$(e_i)$
is democratic with constant
![]() $\Delta $
if
$\Delta $
if
![]() $\Phi (|A|) \le \Delta \lambda (A)$
for all finite
$\Phi (|A|) \le \Delta \lambda (A)$
for all finite
![]() $A \subset \mathbb {N}$
. Democratic bases were introduced in [Reference Konyagin and Temlyakov12] in order to prove the celebrated characterization of greedy bases as unconditional and democratic.
$A \subset \mathbb {N}$
. Democratic bases were introduced in [Reference Konyagin and Temlyakov12] in order to prove the celebrated characterization of greedy bases as unconditional and democratic.
We say that
![]() $(e_i)$
is unconditional for constant coefficients if there exists
$(e_i)$
is unconditional for constant coefficients if there exists
![]() $C>0$
such that, for all finite
$C>0$
such that, for all finite
![]() $A \subset \mathbb {N}$
and all choices of signs
$A \subset \mathbb {N}$
and all choices of signs
![]() $\pm $
,
$\pm $
,
 $$ \begin{align*} \frac{1}{C} \lambda(A) \le \left\|\sum_{i \in A} \pm e_i\right\| \le C\ \lambda (A). \end{align*} $$
$$ \begin{align*} \frac{1}{C} \lambda(A) \le \left\|\sum_{i \in A} \pm e_i\right\| \le C\ \lambda (A). \end{align*} $$
Now suppose that
![]() $(e_i)$
is a Schauder basis for X with biorthogonal functionals
$(e_i)$
is a Schauder basis for X with biorthogonal functionals
![]() $(e_i^*) \subset X^*$
. Let
$(e_i^*) \subset X^*$
. Let
![]() $(\Phi ^*(n))$
be the fundamental function of
$(\Phi ^*(n))$
be the fundamental function of
![]() $(e_i^*)$
. We say that
$(e_i^*)$
. We say that
![]() $(e_i)$
is bidemocratic if
$(e_i)$
is bidemocratic if
(We write
![]() $a_n \asymp b_n$
if there exists
$a_n \asymp b_n$
if there exists
![]() $C>0$
such that
$C>0$
such that
![]() $a_n/C \le b_n \le Ca_n$
for all
$a_n/C \le b_n \le Ca_n$
for all
![]() $n\in \mathbb {N}$
.) It is known that if
$n\in \mathbb {N}$
.) It is known that if
![]() $(e_i)$
is bidemocratic, then both
$(e_i)$
is bidemocratic, then both
![]() $(e_i)$
and
$(e_i)$
and
![]() $(e_i^*)$
are democratic and unconditional for constant coefficients [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 4.2]. Moreover, every subsymmetric basis is bidemocratic [Reference Lindenstrauss and Tzafriri13, Proposition 3.a.6].
$(e_i^*)$
are democratic and unconditional for constant coefficients [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 4.2]. Moreover, every subsymmetric basis is bidemocratic [Reference Lindenstrauss and Tzafriri13, Proposition 3.a.6].
Remark 2.1 As is well known, if
![]() $(e_i)$
is bidemocratic and
$(e_i)$
is bidemocratic and
![]() $(\Phi (n))$
is bounded, then there exists
$(\Phi (n))$
is bounded, then there exists
![]() $C>0$
such that
$C>0$
such that
![]() $\|\sum _{i-1}^n \pm e_i\| \le C$
for all
$\|\sum _{i-1}^n \pm e_i\| \le C$
for all
![]() $n\ge 1$
and for all choices of signs. Hence
$n\ge 1$
and for all choices of signs. Hence
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
. On the other hand, if
$c_0$
. On the other hand, if
![]() $(e_i)$
is bidemocratic and
$(e_i)$
is bidemocratic and
![]() $\Phi (n) \asymp n$
, then
$\Phi (n) \asymp n$
, then
![]() $(\Phi ^*(n))$
is bounded. Hence,
$(\Phi ^*(n))$
is bounded. Hence,
![]() $(e^*_i)$
is equivalent to the u.v.b. of
$(e^*_i)$
is equivalent to the u.v.b. of
![]() $c_0$
. By duality,
$c_0$
. By duality,
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
.
$\ell _1$
.
Example 2.2 (1) For
![]() $1<p<\infty $
, let
$1<p<\infty $
, let
![]() $(e_i)$
be the u.v.b. of p-convexified Tsirelson space
$(e_i)$
be the u.v.b. of p-convexified Tsirelson space
![]() $T_p$
[Reference Figiel and Johnson10]. Then
$T_p$
[Reference Figiel and Johnson10]. Then
![]() $(e_i)$
is democratic and unconditional and
$(e_i)$
is democratic and unconditional and
![]() $\Phi (n) \asymp n^{1/p}$
. Since
$\Phi (n) \asymp n^{1/p}$
. Since
![]() $(n^{1/p})$
has the upper regularity property (see [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, p. 586]), it follows from [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 5.4] that
$(n^{1/p})$
has the upper regularity property (see [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, p. 586]), it follows from [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 5.4] that
![]() $(e_i)$
is bidemocratic. Moreover, from the special properties of block bases in
$(e_i)$
is bidemocratic. Moreover, from the special properties of block bases in
![]() $T_p$
[Reference Casazza and Shura7, Corollary II.5], it follows that there exists
$T_p$
[Reference Casazza and Shura7, Corollary II.5], it follows that there exists
![]() $K>0$
such that for all
$K>0$
such that for all
![]() $\alpha , \beta \in \operatorname {span}((e_i))$
,
$\alpha , \beta \in \operatorname {span}((e_i))$
,
(2) Let
![]() $(e_i)$
be a subsymmetric basis and suppose that all subsymmetric block bases of
$(e_i)$
be a subsymmetric basis and suppose that all subsymmetric block bases of
![]() $(e_i)$
are equivalent to
$(e_i)$
are equivalent to
![]() $(e_i)$
. Altshuler [Reference Altshuler4] constructed the first symmetric example of this type (other than the u.v.b. of
$(e_i)$
. Altshuler [Reference Altshuler4] constructed the first symmetric example of this type (other than the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
). A second symmetric example was constructed in [Reference Casazza and Shura7]. Recently, the first example of a subsymmetric basis of this type, which in addition is not symmetric, was constructed in [Reference Casazza, Dilworth, Kutzarova and Motakis6].
$\ell _p$
). A second symmetric example was constructed in [Reference Casazza and Shura7]. Recently, the first example of a subsymmetric basis of this type, which in addition is not symmetric, was constructed in [Reference Casazza, Dilworth, Kutzarova and Motakis6].
It was proved in [Reference Casazza, Dilworth, Kutzarova and Motakis6, Lemma 17] that if
![]() $(e_i)$
is any subsymmetric basis of this type, then there exists
$(e_i)$
is any subsymmetric basis of this type, then there exists
![]() $K>0$
such that for all
$K>0$
such that for all
![]() $\alpha ^*, \beta ^* \in \operatorname {span}((e^*_i))$
,
$\alpha ^*, \beta ^* \in \operatorname {span}((e^*_i))$
,
Remark 2.3 Suppose that
![]() $(e_i)$
is a basis that satisfies (1.2) with constant K. Then, there exists a constant
$(e_i)$
is a basis that satisfies (1.2) with constant K. Then, there exists a constant
![]() $\tilde K$
such that for every
$\tilde K$
such that for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\alpha \in \operatorname {span}((e_i))$
,
$\alpha \in \operatorname {span}((e_i))$
,
![]() $\alpha ^* \in \operatorname {span}((e^*_i))$
,
$\alpha ^* \in \operatorname {span}((e^*_i))$
,
Note that the left inequality follows simply by iterating (1.2). For the right one, assume without loss of generality that
![]() $(e_i)$
is normalized and monotone. First, make the following easy observation. If
$(e_i)$
is normalized and monotone. First, make the following easy observation. If
![]() $a = \sum _{i=1}^ma_ie_i$
and
$a = \sum _{i=1}^ma_ie_i$
and
![]() $a^* = \sum _{i=1}^mb_ie_i^*$
with
$a^* = \sum _{i=1}^mb_ie_i^*$
with
![]() $a_m\neq 0$
and
$a_m\neq 0$
and
![]() $b_m\neq 0$
, then, for all
$b_m\neq 0$
, then, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $a^{*n}(a^n) = (a^*(a))^n$
.
$a^{*n}(a^n) = (a^*(a))^n$
.
Next, take an
![]() $a^* = \sum _{i=1}^mb_ie_i^*$
and
$a^* = \sum _{i=1}^mb_ie_i^*$
and
![]() $n\in \mathbb {N}$
. By monotonicity, find a norm-one
$n\in \mathbb {N}$
. By monotonicity, find a norm-one
![]() $a = \sum _{i=1}^\ell a_ie_i$
with
$a = \sum _{i=1}^\ell a_ie_i$
with
![]() $\ell \leq m$
such that
$\ell \leq m$
such that
![]() $a^*(a) = \|a^*\|_*$
. Assume first that
$a^*(a) = \|a^*\|_*$
. Assume first that
![]() $\ell < m$
. For
$\ell < m$
. For
![]() $\varepsilon> 0$
, let
$\varepsilon> 0$
, let
![]() $a_\varepsilon = a + \varepsilon e_m$
and note that
$a_\varepsilon = a + \varepsilon e_m$
and note that
![]() $|a^*(a_\varepsilon )| \geq (1-\varepsilon )\|a^*\|_*$
, while
$|a^*(a_\varepsilon )| \geq (1-\varepsilon )\|a^*\|_*$
, while
![]() $\|a_\varepsilon \| \leq 1 + \varepsilon $
. Therefore,
$\|a_\varepsilon \| \leq 1 + \varepsilon $
. Therefore,
and let
![]() $\varepsilon {\to } 0$
. If
$\varepsilon {\to } 0$
. If
![]() $\ell =m$
, the argument is slightly simpler and does not require the perturbation of a.
$\ell =m$
, the argument is slightly simpler and does not require the perturbation of a.
3 Bidemocratic bases
The main theorem of this section is the following.
Theorem 3.1 Suppose that
![]() $(e_i)$
is a bidemocratic basis for X that satisfies (1.2). Then
$(e_i)$
is a bidemocratic basis for X that satisfies (1.2). Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
The above is an immediate consequence of the next proposition and Remark 2.3.
Proposition 3.2 Suppose that
![]() $(e_i)$
is a bidemocratic basis for X that satisfies (2.2). Then
$(e_i)$
is a bidemocratic basis for X that satisfies (2.2). Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() ${\ell }_p$
.
${\ell }_p$
.
Proof For
![]() $n \ge 1$
, let
$n \ge 1$
, let
![]() $\lambda (n) = \|\sum _{i=1}^n e_i\|$
and
$\lambda (n) = \|\sum _{i=1}^n e_i\|$
and
![]() $\lambda ^*(n) =\|\sum _{i=1}^n e^*_i\|_*$
. Note that if
$\lambda ^*(n) =\|\sum _{i=1}^n e^*_i\|_*$
. Note that if
![]() $\alpha = \sum _{i=1}^n e_i$
and
$\alpha = \sum _{i=1}^n e_i$
and
![]() $k \ge 1$
, then
$k \ge 1$
, then
![]() $\alpha ^k = \sum _{i=1}^{n^k}e_i$
. So (2.2) applied to
$\alpha ^k = \sum _{i=1}^{n^k}e_i$
. So (2.2) applied to
![]() $ \alpha $
yields
$ \alpha $
yields
Similarly (2.2) applied to
![]() $\alpha ^* = \sum _{i=1}^n e_i^*$
gives
$\alpha ^* = \sum _{i=1}^n e_i^*$
gives
Since
![]() $(e_i)$
is bidemocratic, there exists
$(e_i)$
is bidemocratic, there exists
![]() $C>0$
such that
$C>0$
such that
Hence,
 $$ \begin{align*}\left[\frac{n}{\lambda(n)}\right]^k \le CK^k \frac{n^k}{\lambda(n^k)},\end{align*} $$
$$ \begin{align*}\left[\frac{n}{\lambda(n)}\right]^k \le CK^k \frac{n^k}{\lambda(n^k)},\end{align*} $$
i.e.,
By the proof (see page 60) of [Reference Lindenstrauss and Tzafriri13, Theorem 2.a.9], (3.1) and (3.2) imply that
![]() $\lambda (n) \asymp n^{1/p}$
for some
$\lambda (n) \asymp n^{1/p}$
for some
![]() $1 \le p \le \infty $
. Since
$1 \le p \le \infty $
. Since
![]() $(e_i)$
is bidemocratic, it follows that
$(e_i)$
is bidemocratic, it follows that
![]() $\Phi (n) \asymp n^{1/p}$
and
$\Phi (n) \asymp n^{1/p}$
and
![]() $\Phi ^*(n) \asymp n^{1/q}$
, where
$\Phi ^*(n) \asymp n^{1/q}$
, where
![]() $q=p/(p-1)$
. By Remark 2.1, if
$q=p/(p-1)$
. By Remark 2.1, if
![]() $p=1$
or
$p=1$
or
![]() $p=\infty $
, then
$p=\infty $
, then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
or
$\ell _1$
or
![]() $c_0$
, respectively.
$c_0$
, respectively.
So suppose that
![]() $1<p<\infty $
. Consider
$1<p<\infty $
. Consider
![]() $\alpha = \sum _{i=1}^m a_i e_i \in \operatorname {span}((e_i))$
. By (2.2),
$\alpha = \sum _{i=1}^m a_i e_i \in \operatorname {span}((e_i))$
. By (2.2),
![]() $\|\alpha \|^n \le K^n \|\alpha ^n\|$
for each
$\|\alpha \|^n \le K^n \|\alpha ^n\|$
for each
![]() $n \ge 1$
. Note that
$n \ge 1$
. Note that
 $$ \begin{align*}\alpha^n = \sum_{i_1+\dots +i_m =n} a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}\bigg(\sum_{j \in A(i_1,\dots,i_m)} e_j\bigg),\end{align*} $$
$$ \begin{align*}\alpha^n = \sum_{i_1+\dots +i_m =n} a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}\bigg(\sum_{j \in A(i_1,\dots,i_m)} e_j\bigg),\end{align*} $$
where
Hence,
 $$ \begin{align*} \|\alpha^n\| &\le \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \lambda(|A(i_1,\dots,i_m)|)\\ & \le \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \Phi(|A(i_1,\dots,i_m)|)\\&\le C \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \binom{n}{i_1 \dots i_m}^{1/p} \end{align*} $$
$$ \begin{align*} \|\alpha^n\| &\le \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \lambda(|A(i_1,\dots,i_m)|)\\ & \le \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \Phi(|A(i_1,\dots,i_m)|)\\&\le C \sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}| \binom{n}{i_1 \dots i_m}^{1/p} \end{align*} $$
(for some
![]() $C>0$
)
$C>0$
)
 $$ \begin{align*} &\le C(n+1)^{m/q}\bigg(\sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}|^p \binom{n}{i_1 \dots i_m}\bigg)^{1/p} \end{align*} $$
$$ \begin{align*} &\le C(n+1)^{m/q}\bigg(\sum_{i_1+\dots+ i_m =n} |a_1^{i_1}a_2^{i_2}\cdots a_m^{i_m}|^p \binom{n}{i_1 \dots i_m}\bigg)^{1/p} \end{align*} $$
by Hölder’s inequality. Hence,
 $$ \begin{align*}\|\alpha\|^n \le K^n C (n+1)^{m/q} \bigg(\sum_{i=1}^m |a_i|^p\bigg)^{n/p}.\end{align*} $$
$$ \begin{align*}\|\alpha\|^n \le K^n C (n+1)^{m/q} \bigg(\sum_{i=1}^m |a_i|^p\bigg)^{n/p}.\end{align*} $$
Taking the nth root and then the limit as
![]() $n \rightarrow \infty $
gives
$n \rightarrow \infty $
gives
 $$ \begin{align} \left\|\sum_{i=1}^m a_i e_i\right\| \le K \bigg(\sum_{i=1}^m |a_i|^p\bigg)^{1/p}.\end{align} $$
$$ \begin{align} \left\|\sum_{i=1}^m a_i e_i\right\| \le K \bigg(\sum_{i=1}^m |a_i|^p\bigg)^{1/p}.\end{align} $$
Since
![]() $(e_i^*)$
also satisfies (2.2) and
$(e_i^*)$
also satisfies (2.2) and
![]() $\Phi ^*(n) \asymp n^{1/q}$
, the same argument gives
$\Phi ^*(n) \asymp n^{1/q}$
, the same argument gives
 $$ \begin{align} \left\|\sum_{i=1}^m a_i e^*_i\right\|_* \le K \bigg(\sum_{i=1}^m |a_i|^q\bigg)^{1/q}. \end{align} $$
$$ \begin{align} \left\|\sum_{i=1}^m a_i e^*_i\right\|_* \le K \bigg(\sum_{i=1}^m |a_i|^q\bigg)^{1/q}. \end{align} $$
Hence, by duality,
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _p$
.
$\ell _p$
.
The following corollary replaces (2.2) by a weaker condition but adds an assumption about the fundamental function.
Corollary 3.3 Let
![]() $1 < p < \infty $
. Suppose that
$1 < p < \infty $
. Suppose that
![]() $(e_i)$
is a bidemocratic basis for X such that
$(e_i)$
is a bidemocratic basis for X such that
![]() $\Phi (n) \asymp n^{1/p}$
. Suppose also that there exists
$\Phi (n) \asymp n^{1/p}$
. Suppose also that there exists
![]() $K>0$
such that for all
$K>0$
such that for all
![]() $\alpha \in \operatorname {span}((e_i))$
and
$\alpha \in \operatorname {span}((e_i))$
and
![]() $\alpha ^* \in \operatorname {span}((e^*_i))$
,
$\alpha ^* \in \operatorname {span}((e^*_i))$
,
Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _p$
.
$\ell _p$
.
4 A characterization of
 $\ell _1$
$\ell _1$
Theorem 4.1 Let
![]() $(e_i)$
be a semi-normalized basis for X. Suppose that there exists
$(e_i)$
be a semi-normalized basis for X. Suppose that there exists
![]() $K>0$
such that, for all
$K>0$
such that, for all
![]() $\alpha ,\beta \in \operatorname {span}((e_i))$
,
$\alpha ,\beta \in \operatorname {span}((e_i))$
,
and also that
 $$ \begin{align} \limsup \frac{1}{n}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^n \pm e_i\right\|>0. \end{align} $$
$$ \begin{align} \limsup \frac{1}{n}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^n \pm e_i\right\|>0. \end{align} $$
Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
.
$\ell _1$
.
Remark 4.2 Note that (1.2) implies that
![]() $\lambda (n) \asymp n^{1/p}$
for some
$\lambda (n) \asymp n^{1/p}$
for some
![]() $1 \le p \le \infty $
(see (5.1)). If
$1 \le p \le \infty $
(see (5.1)). If
![]() $p=1$
and
$p=1$
and
![]() $(e_i)$
is unconditional for constant coefficients, then (4.2) is satisfied. So Theorem 4.1 gives a positive answer to Question 1.1 in this case.
$(e_i)$
is unconditional for constant coefficients, then (4.2) is satisfied. So Theorem 4.1 gives a positive answer to Question 1.1 in this case.
Proof We may assume that
![]() $\|e_i\| \le 1$
for all
$\|e_i\| \le 1$
for all
![]() $i \ge 1$
. By assumption, there exist an infinite
$i \ge 1$
. By assumption, there exist an infinite
![]() $M \subseteq \mathbb {N}$
and
$M \subseteq \mathbb {N}$
and
![]() $\delta>0$
such that
$\delta>0$
such that
 $$ \begin{align*}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^m \pm e_i\right\|>\delta m\end{align*} $$
$$ \begin{align*}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^m \pm e_i\right\|>\delta m\end{align*} $$
for all
![]() $m \in M$
. By Elton’s “
$m \in M$
. By Elton’s “
![]() $\ell _1^n$
theorem” [Reference Elton9], there exist
$\ell _1^n$
theorem” [Reference Elton9], there exist
![]() $\delta _1>0$
and
$\delta _1>0$
and
![]() $c>0$
such that for each
$c>0$
such that for each
![]() $m \in M$
there exists
$m \in M$
there exists
![]() $A_m \subset \{1,2,\dots ,m\}$
, with
$A_m \subset \{1,2,\dots ,m\}$
, with
![]() $|A_m| \ge \delta _1 m$
, such that for all scalars
$|A_m| \ge \delta _1 m$
, such that for all scalars
![]() $(a_i)_{i \in A_m}$
,
$(a_i)_{i \in A_m}$
,
 $$ \begin{align*}c \sum_{i \in A_m} |a_i| \le \left\|\sum_{i \in A_m} a_i e_i\right\| \le \sum_{i \in A_m} |a_i|.\end{align*} $$
$$ \begin{align*}c \sum_{i \in A_m} |a_i| \le \left\|\sum_{i \in A_m} a_i e_i\right\| \le \sum_{i \in A_m} |a_i|.\end{align*} $$
Let
![]() $k \in \mathbb {N}$
. By Szemerédi’s theorem [Reference Szemerédi14], when m is sufficiently large
$k \in \mathbb {N}$
. By Szemerédi’s theorem [Reference Szemerédi14], when m is sufficiently large
![]() $A_m$
contains an arithmetic progression of length k,
$A_m$
contains an arithmetic progression of length k,
![]() $\{n_1, n_1+d, n_1+2d,\dots , n_1+(k-1)d\}$
. Let
$\{n_1, n_1+d, n_1+2d,\dots , n_1+(k-1)d\}$
. Let
![]() $n_1 = bd + r$
, where
$n_1 = bd + r$
, where
![]() $1 \le r \le d$
. Fix scalars
$1 \le r \le d$
. Fix scalars
![]() $(a_i)_{i=1}^k$
and
$(a_i)_{i=1}^k$
and
![]() $\varepsilon>0$
, and set
$\varepsilon>0$
, and set
 $$ \begin{align*}\alpha = \sum_{i=1}^k a_i e_{b+i}\quad\text{and}\quad \beta_\varepsilon=e_r + \varepsilon \sum_{i=r+1}^d e_i.\end{align*} $$
$$ \begin{align*}\alpha = \sum_{i=1}^k a_i e_{b+i}\quad\text{and}\quad \beta_\varepsilon=e_r + \varepsilon \sum_{i=r+1}^d e_i.\end{align*} $$
Note that
 $$ \begin{align*}\alpha\otimes \beta _\varepsilon= \sum_{i=1}^k a_i e_{n_1+(i-1)d} + \varepsilon y\end{align*} $$
$$ \begin{align*}\alpha\otimes \beta _\varepsilon= \sum_{i=1}^k a_i e_{n_1+(i-1)d} + \varepsilon y\end{align*} $$
for some
![]() $y \in \operatorname {span}((e_i))$
. Thus, applying (4.1),
$y \in \operatorname {span}((e_i))$
. Thus, applying (4.1),
 $$ \begin{align*} c\sum_{i=1}^k |a_i| - \varepsilon \|y\| \le \|\alpha \otimes \beta_\varepsilon\| \le K \|\alpha\| \|\beta_\varepsilon\| \le K(1 + (d-r)\varepsilon)\|\alpha\|. \end{align*} $$
$$ \begin{align*} c\sum_{i=1}^k |a_i| - \varepsilon \|y\| \le \|\alpha \otimes \beta_\varepsilon\| \le K \|\alpha\| \|\beta_\varepsilon\| \le K(1 + (d-r)\varepsilon)\|\alpha\|. \end{align*} $$
Taking the limit as
![]() $\varepsilon \rightarrow 0$
, we get
$\varepsilon \rightarrow 0$
, we get
 $$ \begin{align*}\|\alpha\| \ge \frac{c}{K} \sum_{i=1}^k |a_i|.\end{align*} $$
$$ \begin{align*}\|\alpha\| \ge \frac{c}{K} \sum_{i=1}^k |a_i|.\end{align*} $$
Let
![]() $n = \lfloor k/3 \rfloor $
. There exists
$n = \lfloor k/3 \rfloor $
. There exists
![]() $s \in \mathbb {N}$
such that
$s \in \mathbb {N}$
such that
![]() $[(s-1)n +1,sn] \subset [b+1,b+k]$
. We may assume that
$[(s-1)n +1,sn] \subset [b+1,b+k]$
. We may assume that
![]() $a_n \ne 0$
. Then, applying (4.1) again,
$a_n \ne 0$
. Then, applying (4.1) again,
 $$ \begin{align*}\left\|\sum_{i=1}^n a_ie_i\right\| \ge \frac{1}{K} \left\|e_s \otimes \sum_{i=1}^n a_i e_i\right\|=\frac{1}{K}\left\|\sum_{i=1}^n a_i e_{(s-1)n+i}\right\| \ge \frac{c}{K^2}\sum_{i=1}^n |a_i|.\end{align*} $$
$$ \begin{align*}\left\|\sum_{i=1}^n a_ie_i\right\| \ge \frac{1}{K} \left\|e_s \otimes \sum_{i=1}^n a_i e_i\right\|=\frac{1}{K}\left\|\sum_{i=1}^n a_i e_{(s-1)n+i}\right\| \ge \frac{c}{K^2}\sum_{i=1}^n |a_i|.\end{align*} $$
Since k (and hence n) are arbitrary, it follows that
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
.
$\ell _1$
.
Corollary 4.3 Suppose that
![]() $(e_i)$
satisfies (4.1) and is unconditional for constant coefficients and that
$(e_i)$
satisfies (4.1) and is unconditional for constant coefficients and that
![]() $\lambda (n) \asymp n$
. Then
$\lambda (n) \asymp n$
. Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
.
$\ell _1$
.
Remark 4.4 Corollary 4.3 does not admit an
![]() $\ell _p$
version for
$\ell _p$
version for
![]() $p>1$
. To see this, let
$p>1$
. To see this, let
![]() $q = p/(p-1)$
. As observed in Example 2.2, the u.v.b.
$q = p/(p-1)$
. As observed in Example 2.2, the u.v.b.
![]() $(e_i)$
of
$(e_i)$
of
![]() $T_q^*$
is unconditional and bidemocratic with
$T_q^*$
is unconditional and bidemocratic with
![]() $\phi (n) \asymp n^{1/p}$
. Moreover, (2.1) dualizes due to the special property of block bases of
$\phi (n) \asymp n^{1/p}$
. Moreover, (2.1) dualizes due to the special property of block bases of
![]() $T_q$
[Reference Casazza and Shura7, Corollary II.5]. In particular,
$T_q$
[Reference Casazza and Shura7, Corollary II.5]. In particular,
![]() $(e_i)$
satisfies (4.1). Thus, Corollary 4.3 does not admit an
$(e_i)$
satisfies (4.1). Thus, Corollary 4.3 does not admit an
![]() $\ell _p$
version for
$\ell _p$
version for
![]() $p>1$
.
$p>1$
.
5 Democratic bases
Democratic bases are more general than bidemocratic bases. In this section, we prove a characterization of the u.v.b. of
![]() $\ell _p$
or
$\ell _p$
or
![]() $c_0$
among democratic bases.
$c_0$
among democratic bases.
The characterization involves the notion of quasi-greedy basis which we now recall. Let
![]() $(e_i)$
be a basis for X. For
$(e_i)$
be a basis for X. For
![]() $x \in X$
and
$x \in X$
and
![]() $\delta>0$
, let
$\delta>0$
, let
Then
![]() $(e_i)$
is quasi-greedy if there exists
$(e_i)$
is quasi-greedy if there exists
![]() $A>0$
such that for all
$A>0$
such that for all
![]() $x \in X$
and for all
$x \in X$
and for all
![]() $\delta>0$
,
$\delta>0$
,
![]() $\|\mathcal {G}_\delta (x)\| \le A \|x\|$
. Quasi-greedy bases were introduced in [Reference Konyagin and Temlyakov12] in connection with the Thresholding Greedy Algorithm. While unconditional bases are quasi-greedy, there are also important examples of conditional quasi-greedy bases [Reference Albiac, Ansorena, Dilworth and Kutzarova1, Reference Konyagin and Temlyakov12, Reference Wojtaszczyk16]. However, quasi-greedy bases are always unconditional for constant coefficients [Reference Wojtaszczyk16]. We refer to [Reference Dilworth, Kutzarova, Knealton and Temlyakov8] for the definition of an almost greedy basis. Almost greediness of a basis is proved in [Reference Dilworth, Kutzarova, Knealton and Temlyakov8] to be equivalent to being quasi-greedy and democratic.
$\|\mathcal {G}_\delta (x)\| \le A \|x\|$
. Quasi-greedy bases were introduced in [Reference Konyagin and Temlyakov12] in connection with the Thresholding Greedy Algorithm. While unconditional bases are quasi-greedy, there are also important examples of conditional quasi-greedy bases [Reference Albiac, Ansorena, Dilworth and Kutzarova1, Reference Konyagin and Temlyakov12, Reference Wojtaszczyk16]. However, quasi-greedy bases are always unconditional for constant coefficients [Reference Wojtaszczyk16]. We refer to [Reference Dilworth, Kutzarova, Knealton and Temlyakov8] for the definition of an almost greedy basis. Almost greediness of a basis is proved in [Reference Dilworth, Kutzarova, Knealton and Temlyakov8] to be equivalent to being quasi-greedy and democratic.
Theorem 5.1 Let
![]() $(e_i)$
be a quasi-greedy democratic (i.e., almost greedy) basis for X which satisfies (1.2). Then
$(e_i)$
be a quasi-greedy democratic (i.e., almost greedy) basis for X which satisfies (1.2). Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
Proof By considering
![]() $\alpha = \sum _{i=1}^m e_i$
and
$\alpha = \sum _{i=1}^m e_i$
and
![]() $\beta {\kern-1.2pt}={\kern-1.2pt} \sum _{i=1}^n e_i$
, (1.2) implies that, for all
$\beta {\kern-1.2pt}={\kern-1.2pt} \sum _{i=1}^n e_i$
, (1.2) implies that, for all
![]() $m,n {\kern-1.2pt}\in{\kern-1.2pt} \mathbb {N}$
,
$m,n {\kern-1.2pt}\in{\kern-1.2pt} \mathbb {N}$
,
Hence, by [Reference Lindenstrauss and Tzafriri13],
![]() $\lambda (n) \asymp n^{1/p}$
for some
$\lambda (n) \asymp n^{1/p}$
for some
![]() $1 \le p \le \infty $
. Since
$1 \le p \le \infty $
. Since
![]() $(e_i)$
is democratic, it follows that
$(e_i)$
is democratic, it follows that
![]() $\Phi (n) \asymp n^{1/p}$
.
$\Phi (n) \asymp n^{1/p}$
.
If
![]() $(\Phi (n))$
is bounded, then, since
$(\Phi (n))$
is bounded, then, since
![]() $(e_i)$
is unconditional for constant coefficients, there exists
$(e_i)$
is unconditional for constant coefficients, there exists
![]() $C>0$
such that
$C>0$
such that
![]() $\|\sum _{i=1}^n \pm e_i\| \le C$
for all
$\|\sum _{i=1}^n \pm e_i\| \le C$
for all
![]() $n \ge 1$
and all choices of signs. Hence,
$n \ge 1$
and all choices of signs. Hence,
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
.
$c_0$
.
If
![]() $\phi (n) \asymp n$
, then by the democratic assumption and unconditionality for constant coefficients, it follows that
$\phi (n) \asymp n$
, then by the democratic assumption and unconditionality for constant coefficients, it follows that
 $$ \begin{align*}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^n \pm e_i\right\| \asymp n.\end{align*} $$
$$ \begin{align*}\underset{\pm}{\operatorname{Ave}}\left\|\sum_{i=1}^n \pm e_i\right\| \asymp n.\end{align*} $$
Hence, by Theorem 4.1,
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $\ell _1$
.
$\ell _1$
.
So suppose that
![]() $1<p<\infty $
. The sequence
$1<p<\infty $
. The sequence
![]() $(n^{1/p})$
has the “upper regularity property” for
$(n^{1/p})$
has the “upper regularity property” for
![]() $1<p<\infty $
(see [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, p. 586]). So
$1<p<\infty $
(see [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, p. 586]). So
![]() $(e_i)$
is quasi-greedy and democratic and
$(e_i)$
is quasi-greedy and democratic and
![]() $(\Phi (n))$
has the upper regularity property. Hence, by [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 4.4],
$(\Phi (n))$
has the upper regularity property. Hence, by [Reference Dilworth, Kutzarova, Knealton and Temlyakov8, Proposition 4.4],
![]() $(e_i)$
is bidemocratic. In particular,
$(e_i)$
is bidemocratic. In particular,
![]() $\Phi ^*(n) \asymp n^{1/q}$
, where
$\Phi ^*(n) \asymp n^{1/q}$
, where
![]() $q=p/(p-1)$
.
$q=p/(p-1)$
.
The proof is now concluded as in Proposition 3.2. More precisely, the left-hand inequality of (1.2) gives an upper p-estimate for
![]() $(e_i)$
and (2.3) gives an upper q-estimate for
$(e_i)$
and (2.3) gives an upper q-estimate for
![]() $(e_i^*)$
.
$(e_i^*)$
.
6 Subsequences
In this section, we use results from the theory of spreading models initiated by Brunel and Sucheston [Reference Brunel and Sucheston5]. We start with a brief review. A basic sequence
![]() $(e_i)$
is invariant under spreading (IS) if there exists
$(e_i)$
is invariant under spreading (IS) if there exists
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*}\frac{1}{C} \left\|\sum_{i=1}^n a_i e_i\right\| \le \left\| \sum _{j=1}^n a_j e_{i_j}\right\| \le C \left\|\sum_{i=1}^n a_i e_i\right\|\end{align*} $$
$$ \begin{align*}\frac{1}{C} \left\|\sum_{i=1}^n a_i e_i\right\| \le \left\| \sum _{j=1}^n a_j e_{i_j}\right\| \le C \left\|\sum_{i=1}^n a_i e_i\right\|\end{align*} $$
for all
![]() $n \ge 1$
,
$n \ge 1$
,
![]() $i_1<\cdots <i_n$
, and scalars
$i_1<\cdots <i_n$
, and scalars
![]() $(a_i)_{i=1}^n$
.
$(a_i)_{i=1}^n$
.
We say
![]() $(e_i)$
generates a spreading model if there exists a Banach space
$(e_i)$
generates a spreading model if there exists a Banach space
![]() $(Y,\|\cdot \|_Y)$
with basis
$(Y,\|\cdot \|_Y)$
with basis
![]() $(s_i)$
such that
$(s_i)$
such that
 $$ \begin{align*}\left\|\sum_{i=1}^n a_i s_i\right\|_Y = \underset{i_1 <\cdots<i_n}{\lim_{i_1 \rightarrow \infty}}\left\|\sum_{j=1}^n a_j e_{i_j}\right\|\end{align*} $$
$$ \begin{align*}\left\|\sum_{i=1}^n a_i s_i\right\|_Y = \underset{i_1 <\cdots<i_n}{\lim_{i_1 \rightarrow \infty}}\left\|\sum_{j=1}^n a_j e_{i_j}\right\|\end{align*} $$
for all
![]() $n\ge 1$
and scalars
$n\ge 1$
and scalars
![]() $(a_i)_{i=1}^n$
. It was proved in [Reference Brunel and Sucheston5] that every basic sequence has a subsequence
$(a_i)_{i=1}^n$
. It was proved in [Reference Brunel and Sucheston5] that every basic sequence has a subsequence
![]() $(x_i)$
which generates a spreading model. Note that
$(x_i)$
which generates a spreading model. Note that
![]() $(s_i)$
is IS with
$(s_i)$
is IS with
![]() $C=1$
. Moreover,
$C=1$
. Moreover,
![]() $(s_{2i}-s_{2i-1})$
is suppression
$(s_{2i}-s_{2i-1})$
is suppression
![]() $1$
-unconditional [Reference Brunel and Sucheston5]. Note that an IS sequence
$1$
-unconditional [Reference Brunel and Sucheston5]. Note that an IS sequence
![]() $(e_i)$
is equivalent to the spreading model
$(e_i)$
is equivalent to the spreading model
![]() $(s_i)$
generated by a subsequence of
$(s_i)$
generated by a subsequence of
![]() $(e_i)$
. Hence
$(e_i)$
. Hence
![]() $(e_{2i}-e_{2i-1})$
is IS and unconditional.
$(e_{2i}-e_{2i-1})$
is IS and unconditional.
Theorem 6.1 Suppose that
![]() $(e_i)$
is IS and satisfies (1.2). Then
$(e_i)$
is IS and satisfies (1.2). Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
Proof As remarked above,
![]() $(e_{2i}-e_{2i-1})$
is IS and unconditional. Because, for every choice of scalars
$(e_{2i}-e_{2i-1})$
is IS and unconditional. Because, for every choice of scalars
![]() $a_1,\ldots ,a_n$
,
$a_1,\ldots ,a_n$
,
 $$\begin{align*}\bigg(\sum_{i=1}^na_ie_i\bigg)\otimes(e_2-e_1) = \sum_{i=1}^na_i(e_{2i}-e_{2i-1}),\end{align*}$$
$$\begin{align*}\bigg(\sum_{i=1}^na_ie_i\bigg)\otimes(e_2-e_1) = \sum_{i=1}^na_i(e_{2i}-e_{2i-1}),\end{align*}$$
(1.2) yields that
![]() $(e_i)_i$
is equivalent to
$(e_i)_i$
is equivalent to
![]() $(e_{2i}-e_{2i-1})$
. Therefore,
$(e_{2i}-e_{2i-1})$
. Therefore,
![]() $(e_i)_i$
is almost greedy and, thus, by Theorem 5.1, the result follows.
$(e_i)_i$
is almost greedy and, thus, by Theorem 5.1, the result follows.
To state the next result, we first make some clarifying remarks to avoid a possible source of confusion. For any given semi-normalized basic sequence
![]() $(e_i)$
, we defined a multiplication
$(e_i)$
, we defined a multiplication
![]() $\otimes $
on
$\otimes $
on
![]() $\operatorname {span}((e_i))$
by (1.1). We must emphasize, however, that for a different choice of basic sequence,
$\operatorname {span}((e_i))$
by (1.1). We must emphasize, however, that for a different choice of basic sequence,
![]() $(f_i)$
say, the corresponding multiplication will also be different. But to avoid cumbersome notation, we use the same symbol
$(f_i)$
say, the corresponding multiplication will also be different. But to avoid cumbersome notation, we use the same symbol
![]() $\otimes $
for both. Likewise, when we say in the next result that all subsequences of
$\otimes $
for both. Likewise, when we say in the next result that all subsequences of
![]() $(e_i)$
satisfy (1.2), it is to be understood that the constant K in (1.2) will depend on the subsequence, i.e., we are not assuming a priori that there is a uniform K for all subsequences. (Of course, as the result shows, a uniform K does in fact exist.)
$(e_i)$
satisfy (1.2), it is to be understood that the constant K in (1.2) will depend on the subsequence, i.e., we are not assuming a priori that there is a uniform K for all subsequences. (Of course, as the result shows, a uniform K does in fact exist.)
Theorem 6.2 Let
![]() $(e_i)$
be a semi-normalized basic sequence. Suppose that every subsequence of
$(e_i)$
be a semi-normalized basic sequence. Suppose that every subsequence of
![]() $(e_i)$
satisfies (1.2). Then
$(e_i)$
satisfies (1.2). Then
![]() $(e_i)$
is equivalent to the u.v.b. of
$(e_i)$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
The proof requires the following lemma.
Lemma 6.3 Let
![]() $(e_i)$
be a semi-normalized basic sequence which satisfies (1.2). Then all sequences of the form
$(e_i)$
be a semi-normalized basic sequence which satisfies (1.2). Then all sequences of the form
![]() $(e_{mn+i})_{i=1}^n$
(
$(e_{mn+i})_{i=1}^n$
(
![]() $m,n \in \mathbb {N}$
) are uniformly equivalent to
$m,n \in \mathbb {N}$
) are uniformly equivalent to
![]() $(e_i)_{i=1}^n$
, i.e., there exists
$(e_i)_{i=1}^n$
, i.e., there exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $m,n \in \mathbb {N}$
and all scalars
$m,n \in \mathbb {N}$
and all scalars
![]() $(a_i)_{i=1}^n$
,
$(a_i)_{i=1}^n$
,
 $$ \begin{align*}\frac{1}{C}\left\|\sum_{i=1}^n a_i e_i\right\| \le \left\|\sum_{i=1}^n a_i e_{mn+i}\right\| \le C \left\|\sum_{i=1}^n a_i e_i\right\|.\end{align*} $$
$$ \begin{align*}\frac{1}{C}\left\|\sum_{i=1}^n a_i e_i\right\| \le \left\|\sum_{i=1}^n a_i e_{mn+i}\right\| \le C \left\|\sum_{i=1}^n a_i e_i\right\|.\end{align*} $$
Proof This follows at once from (1.2) along with the observation that
 $$ \begin{align*}e_{m+1} \otimes \bigg(\sum_{i=1}^n a_i e_i \bigg)= \sum_{i=1}^n a_i e_{mn+i}.\end{align*} $$
$$ \begin{align*}e_{m+1} \otimes \bigg(\sum_{i=1}^n a_i e_i \bigg)= \sum_{i=1}^n a_i e_{mn+i}.\end{align*} $$
Proof of Theorem 6.2
By Theorem 6.1, it suffices to prove that
![]() $(e_i)$
is IS. Let
$(e_i)$
is IS. Let
![]() $(y_i)$
be a subsequence of
$(y_i)$
be a subsequence of
![]() $(e_i)$
which generates a spreading model
$(e_i)$
which generates a spreading model
![]() $(Y, \|\cdot \|_Y)$
with basis
$(Y, \|\cdot \|_Y)$
with basis
![]() $(s_i)$
. We define a subsequence
$(s_i)$
. We define a subsequence
![]() $(x_i)$
of
$(x_i)$
of
![]() $(e_i)$
inductively. For
$(e_i)$
inductively. For
![]() $1 \le i \le 3$
, let
$1 \le i \le 3$
, let
![]() $x_i = e_i$
. For the inductive step, suppose that
$x_i = e_i$
. For the inductive step, suppose that
![]() $n \ge 1$
and that
$n \ge 1$
and that
![]() $(x_i)_{i=1}^{3^n}$
have been defined with
$(x_i)_{i=1}^{3^n}$
have been defined with
![]() $x_i = e_{N(i)}$
, where
$x_i = e_{N(i)}$
, where
![]() $(N(i))_{i=1}^{3^n}$
is strictly increasing. Choose
$(N(i))_{i=1}^{3^n}$
is strictly increasing. Choose
![]() $m \in \mathbb {N}$
with
$m \in \mathbb {N}$
with
![]() $m3^n>N(3^n)$
and define
$m3^n>N(3^n)$
and define
![]() $x_{3^n + i} = e_{m3^n +i}$
for
$x_{3^n + i} = e_{m3^n +i}$
for
![]() $1 \le i \le 3^n$
. Thus,
$1 \le i \le 3^n$
. Thus,
![]() $x_i$
has now been defined for
$x_i$
has now been defined for
![]() $1 \le i \le 2\cdot 3^n$
.
$1 \le i \le 2\cdot 3^n$
.
Now choose
![]() $p> (m+1)3^n$
such that
$p> (m+1)3^n$
such that
 $$ \begin{align} \frac{1}{2}\left\|\sum_{i=1}^{3^n} a_i s_i\right\|_Y \le \left\|\sum_{i=1}^{3^n} a_i y_{p+i}\right\| \le 2 \left\|\sum_{i=1}^{3^n} a_i s_i\right\|_Y \end{align} $$
$$ \begin{align} \frac{1}{2}\left\|\sum_{i=1}^{3^n} a_i s_i\right\|_Y \le \left\|\sum_{i=1}^{3^n} a_i y_{p+i}\right\| \le 2 \left\|\sum_{i=1}^{3^n} a_i s_i\right\|_Y \end{align} $$
for all scalars
![]() $(a_i)_{i=1}^{3^n}$
. This is possible because
$(a_i)_{i=1}^{3^n}$
. This is possible because
![]() $(y_i)$
generates the spreading model with basis
$(y_i)$
generates the spreading model with basis
![]() $(s_i)$
. Define
$(s_i)$
. Define
![]() $x_{2\cdot 3^n+i} = y_{p+i}$
for
$x_{2\cdot 3^n+i} = y_{p+i}$
for
![]() $1 \le i \le 3^n$
. This completes the inductive definition of
$1 \le i \le 3^n$
. This completes the inductive definition of
![]() $x_i = e_{N(i)}$
for
$x_i = e_{N(i)}$
for
![]() $1 \le i \le 3^{n+1}$
. Note that
$1 \le i \le 3^{n+1}$
. Note that
and
Hence,
![]() $(N(i))_{i=1}^{3^{n+1}}$
is strictly increasing as desired.
$(N(i))_{i=1}^{3^{n+1}}$
is strictly increasing as desired.
By assumption,
![]() $(x_i)$
satisfies (1.2) for some
$(x_i)$
satisfies (1.2) for some
![]() $K>0$
. Hence, by Lemma 6.3,
$K>0$
. Hence, by Lemma 6.3,
![]() $(x_{3^n+i})_{i=1}^{3^n} = (e_{m\cdot 3^n+i})_{i=1}^{3^n}$
is uniformly equivalent to
$(x_{3^n+i})_{i=1}^{3^n} = (e_{m\cdot 3^n+i})_{i=1}^{3^n}$
is uniformly equivalent to
![]() $(e_i)_{i=1}^{3^n}$
. Again, by Lemma 6.3,
$(e_i)_{i=1}^{3^n}$
. Again, by Lemma 6.3,
![]() $(x_{3^n+i})_{i=1}^{3^n}$
is uniformly equivalent to
$(x_{3^n+i})_{i=1}^{3^n}$
is uniformly equivalent to
![]() $(x_{2\cdot 3^n+i})_{i=1}^{3^n}$
, which in turn is uniformly equivalent to
$(x_{2\cdot 3^n+i})_{i=1}^{3^n}$
, which in turn is uniformly equivalent to
![]() $(s_i)_{i=1}^{3^n}$
by (6.1). So
$(s_i)_{i=1}^{3^n}$
by (6.1). So
![]() $(e_i)_{i=1}^{3^n}$
is uniformly equivalent to
$(e_i)_{i=1}^{3^n}$
is uniformly equivalent to
![]() $(s_i)_{i=1}^{3^n}$
, i.e.,
$(s_i)_{i=1}^{3^n}$
, i.e.,
![]() $(e_i)$
is equivalent to
$(e_i)$
is equivalent to
![]() $(s_i)$
as desired.
$(s_i)$
as desired.
We conclude with a characterization of basic sequences that are saturated by subsequences equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.
Let
![]() $[\mathbb {N}]^\omega $
denote the collection of increasing sequences
$[\mathbb {N}]^\omega $
denote the collection of increasing sequences
![]() $(n_k)_{k=1}^\infty $
of natural numbers endowed with the product topology.
$(n_k)_{k=1}^\infty $
of natural numbers endowed with the product topology.
Theorem 6.4 Let
![]() $(e_i)$
be a semi-normalized basic sequence. The following are equivalent:
$(e_i)$
be a semi-normalized basic sequence. The following are equivalent:
-
(a) Every subsequence of
 $(e_i)$
contains a further subsequence equivalent to the u.v.b. of
$(e_i)$
contains a further subsequence equivalent to the u.v.b. of
 $c_0$
or
$c_0$
or
 $\ell _p$
.
$\ell _p$
. -
(b) Every subsequence of
 $(e_i)$
contains a further subsequence satisfying (1.2) for some
$(e_i)$
contains a further subsequence satisfying (1.2) for some
 $K>0$
.
$K>0$
.
Proof (a)
![]() $\Rightarrow $
(b) is obvious. Suppose (b) holds. Let
$\Rightarrow $
(b) is obvious. Suppose (b) holds. Let
![]() $(f_i)$
be any subsequence of
$(f_i)$
be any subsequence of
![]() $(e_i)$
. Let
$(e_i)$
. Let
Then B is easily seen to be a Borel set. Hence, by the infinite Ramsey theorem of Galvin and Prikry [Reference Galvin and Prikry11], there exists
![]() $(n_k)_{k=1}^\infty \in [\mathbb {N}]^\omega $
such that either every subsequence of
$(n_k)_{k=1}^\infty \in [\mathbb {N}]^\omega $
such that either every subsequence of
![]() $(n_k)_{k=1}^\infty $
belongs to B or every subsequence belongs to the complement of B. The latter contradicts (b). By Theorem 6.2, the former implies that
$(n_k)_{k=1}^\infty $
belongs to B or every subsequence belongs to the complement of B. The latter contradicts (b). By Theorem 6.2, the former implies that
![]() $(f_{n_k})$
is equivalent to the u.v.b. of
$(f_{n_k})$
is equivalent to the u.v.b. of
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
.
$\ell _p$
.