Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-23T15:57:30.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Independence of Logarithms of Cyclotomic Numbers and a Conjecture of Livingston

Part of: Algebraic number theory: global fields Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  12 December 2019

Tapas Chatterjee  and
Sonika Dhillon
Tapas Chatterjee
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Punjab, India Email: tapasc@iitrpr.ac.insonika@iitrpr.ac.in
Sonika Dhillon
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Punjab, India Email: tapasc@iitrpr.ac.insonika@iitrpr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1965, A. Livingston conjectured the 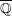$\overline{\mathbb{Q}}$-linear independence of logarithms of values of the sine function at rational arguments. In 2016, S. Pathak disproved the conjecture. In this article, we give a new proof of Livingston’s conjecture using some fundamental trigonometric identities. Moreover, we show that a stronger version of her theorem is true. In fact, we modify this conjecture by introducing a co-primality condition, and in that case we provide the necessary and sufficient conditions for the conjecture to be true. Finally, we identify a maximal linearly independent subset of the numbers considered in Livingston’s conjecture.

Keywords

Baker’s theorylinear forms in logarithmprimitive rootunits in cyclotomic field

MSC classification

Primary: 11J81: Transcendence (general theory)
Secondary: 11J72: Irrationality; linear independence over a field 11J86: Linear forms in logarithms; Baker's method 11J91: Transcendence theory of other special functions 11R27: Units and factorization
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 31 - 45
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, A., Transcendental number theory. Cambridge University Press, London–New York, 1975.CrossRefGoogle Scholar
Bass, H., Dirichlet unit theorem, induced characters, and Whitehead groups of finite groups. Topology 4(1965), 391–410. https://doi.org/10.1016/0040-9383(66)90036-XCrossRefGoogle Scholar
Chatterjee, T. and Dhillon, S., Linear independence of harmonic numbers over the field of algebraic numbers. Ramanujan J. (2019). https://doi.org/10.1007/s11139-018-0124-6CrossRefGoogle Scholar
Chatterjee, T. and Dhillon, S., Linear independence of harmonic numbers over the field of algebraic numbers II. Ramanujan J. https://doi.org/10.1007/s11139-019-00183-8Google Scholar
Chatterjee, T. and Gun, S., The digamma function, Euler–Lehmer constants and their p-adic counterparts. Acta Arith. 162(2014), 197–208. https://doi.org/10.4064/aa162-2-4CrossRefGoogle Scholar
Chatterjee, T. and Murty, M. R., Non-vanishing of Dirichlet series with periodic coefficients. J. Number Theory 145(2014), 1–21. https://doi.org/10.1016/j.jnt.2014.05.010CrossRefGoogle Scholar
Chatterjee, T., Murty, M. R., and Pathak, S., A vanishing criterion for Dirichlet series with periodic coefficients. In: Number theory related to modular curves—Momose memorial volume. Contemp. Math., 701, American Mathematical Society, Providence, RI, 2018, pp. 69–80. https://doi.org/10.1090/conm/701/14141CrossRefGoogle Scholar
Ennola, V., On relations between cyclotomic units. J. Number Theory 4(1972), 236–247. https://doi.org/10.1016/0022-314X(72)90050-9CrossRefGoogle Scholar
Livingston, A., The series ∑n=1∞f (n)/n for periodic f. Canad. Math. Bull. 8(1965), 413–432. https://doi.org/10.4153/CMB-1965-029-2CrossRefGoogle Scholar
Murty, M. R. and Saradha, N., Transcendental values of the p-adic digamma function. Acta Arith. 133(2008), 349–362. https://doi.org/10.4064/aa133-4-4CrossRefGoogle Scholar
Murty, M. R. and Saradha, N., Euler–Lehmer constants and a conjecture of Erdős. J. Number Theory 130(2010), 2671–2682. https://doi.org/10.1016/j.jnt.2010.07.004CrossRefGoogle Scholar
Pathak, S., On a conjecture of Livingston. Canad. Math. Bull. 60(2017), 184–195. https://doi.org/10.4153/CMB-2016-065-1CrossRefGoogle Scholar
Pei, D. Y. and Feng, K., A note on the independence of the cyclotomic units. Acta Math. Sinica 23(1980), 773–778.Google Scholar
Ramachandra, K., On the units of cyclotomic fields. Acta Arith. 12(1966/67), 165–173. https://doi.org/10.4064/aa-12-2-165-173CrossRefGoogle Scholar
Washington, L. C., Introduction to cyclotomic fields, Second ed., Graduate Texts in Mathematics, 83, Springer, New York, 1997. https://doi.org/10.1007/978-1-4612-1934-7CrossRefGoogle Scholar