Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-25T18:06:46.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant Theory of Abelian Transvection Groups

Published online by Cambridge University Press:  20 November 2018

Abraham Broer
Abraham Broer*
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, Montréal, QC H3C 3J7 e-mail: broera@dms.umontreal.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

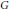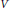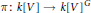Let $G$ be a finite group acting linearly on the vector space $V$ over a field of arbitrary characteristic. The action is called coregular if the invariant ring is generated by algebraically independent homogeneous invariants, and the direct summand property holds if there is a surjective $k{{[V]}^{G}}$-linear map $\pi \,:\,k[V]\,\to \,k{{[V]}^{G}}$.

The following Chevalley–Shephard–Todd type theorem is proved. Suppose 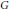$G$ is abelian. Then the action is coregular if and only if 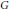$G$ is generated by pseudo-reflections and the direct summand property holds.

Keywords

13A50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 3 , 01 September 2010 , pp. 404 - 411
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Benson, D. J., Polynomial Invariants of Finite Groups. London Mathematical Society Lecture Note Series 190. Cambridge University Press, Cambridge, 1993.Google Scholar
[2] Broer, A., The direct summand property in modular invariant theory. Transform. Groups 10(2005), no. 1, 5–27. doi:10.1007/s00031-005-1001-0Google Scholar
[3] Broer, A., On Chevalley–Shephard–Todd's theorem in positive characteristic. In: Symmetry and spaces, Progress in Mathematics, 278, Birkhäuser, Boston, 2010, pp. 21–34.Google Scholar
[4] Derksen, H. and Kemper, G., Computational invariant theory. Invariant Theory and Algebraic Transformation Groups, I. Encyclopaedia of Mathematical Sciences 130. Springer-Verlag, Berlin, 2002.Google Scholar
[5] Nakajima, H., Invariants of finite groups generated by pseudoreflections in positive characteristic. Tsukuba J. Math. 3(1979), no. 1, 109–122.Google Scholar
[6] Nakajima, H., Modular representations of abelian groups with regular rings of invariants. Nagoya Math. J. 86(1982), 229–248.Google Scholar
[7] Nakajima, H., Regular rings of invariants of unipotent groups. J. Algebra 85(1983), no. 2, 253–286. doi:10.1016/0021-8693(83)90094-7Google Scholar
[8] Shank, R. J. and Wehlau, D. L., The transfer in modular invariant theory. J. Pure Appl. Algebra 142(1999), no. 1, 63–77. doi:10.1016/S0022-4049(98)00036-XGoogle Scholar