Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T03:12:39.359Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding the Hopf Automorphism Group into the Brauer Group

Published online by Cambridge University Press:  20 November 2018

Fred Van Oystaeyen  and
Yinhuo Zhang
Fred Van Oystaeyen
Affiliation:
Department of Mathematics University of Antwerp (UIA) B-2610, Wilrijk Belgium
Yinhuo Zhang
Affiliation:
Department of Mathematics University of Antwerp (UIA) B-2610, Wilrijk Belgium
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

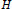Let $H$ be a faithfully projective Hopf algebra over a commutative ring $k$. In [8, 9] we defined the Brauer group 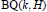$\text{BQ}(k,H)$ of 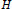$H$ and an homomorphism $\pi $ from Hopf automorphism group 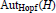$\text{Au}{{\text{t}}_{\text{Hopf}}}(H)$ to 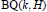$\text{BQ}(k,H)$. In this paper, we show that the morphism $\pi $ can be embedded into an exact sequence.

Keywords

16W3013A20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 3 , 01 September 1998 , pp. 359 - 367
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Beattie, M., The BrauerGroup ofCentral Separable G-Azumaya Algebras. J.Algebra 54 (1978), 516–525.Google Scholar
2. Beattie, M., Computing the Brauer Group of Graded Azumaya Algebras from Its Subgroups. J. Algebra 101 (1986), 339–349.Google Scholar
3. Beattie, M., A direct sum decomposition for the Brauer group of H-module algebras. J. Algebra 43 (1976), 686–693.Google Scholar
4. Blatter, R. J., Cohen, M. and Montgomery, S., Crossed Products and Inner Actions. Trans. Amer.Math. Soc. 298 (1986), 671–711.Google Scholar
5. Caenepeel, S., Computing the Brauer-Long Group of a Hopf Algebra I: The Cohomological Theory. Israel J. Math. 72 (1990), 38–83.Google Scholar
6. Caenepeel, S., Computing the Brauer-Long Group of a Hopf Algebra II: The Skolem-Noether Theory. J. Pure Appl. Alg. 84 (1993), 107–144.Google Scholar
7. Caenepeel, S. and Beattie, M., A Cohomological Approach to the Brauer-Long Group and The Groups of Galois Extensions and Strongly Graded Rings. Trans.Amer.Math. Soc. 324 (1991), 747–775.Google Scholar
8. Caenepeel, S., Van Oystaeyen, F. and Zhang, Y. H., Quantum Yang-Baxter Module Algebras. K-Theory 8, 231–255.Google Scholar
9. Caenepeel, S., Van Oystaeyen, F. and Zhang, Y. H., The Brauer Group of Yetter-Drinfel’d Module algebras. Trans. Amer. Math. Soc., to appear.Google Scholar
10. Deegan, A. P., A Subgroup of the Generalized Brauer Group of Γ-Azumaya Algebras. J. London Math. Soc. 2 (1981), 223–240.Google Scholar
11. Lame, L. A. and Radford, D. E., Algebraic Aspects of the Quantum Yang-Baxter Equation. J. Algebra 154 (1992), 228–288.Google Scholar
12. Long, F. W., A Generalization of the Brauer Group of Graded Algebras. Proc. London Math. Soc. 29 (1974), 237–256.Google Scholar
13. Long, F. W., The Brauer Group of Dimodule Algebras. J.Algebra 31 (1974), 559–601.Google Scholar
14. Majid, S., Doubles of Quasitriangular Hopf Algebras. Comm. Algebra 19 (1991), 3061–3073.Google Scholar
15. Radford, D. E., Minimal Quasitriangular Hopf Algebras. J.Algebra 157 (1993), 285–315.Google Scholar
16. Radford, D. E., The Group of Automorphisms of a Semisimple Hopf Algebra over a Field of Characteristic 0 is Finite. Amer. J.Math. 112 (1990), 331–357.Google Scholar
17. Sweedler, M. E., Hopf Algebras. Benjamin, 1969.Google Scholar
18. Yetter, D. N., Quantum Groups and Representations of Monoidal categories. Math. Proc. Cambridge Philos. Soc. 108 (1990), 261–290.Google Scholar