Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-16T16:12:27.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugacy Classes of Subalgebras of the Real Sedenions

Published online by Cambridge University Press:  20 November 2018

Kai-Cheong Chan  and
Dragomir Ž. Đoković
Kai-Cheong Chan
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: kclchan@math.uwaterloo.ca e-mail: djokovic@uwaterloo.ca
Dragomir Ž. Đoković
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: kclchan@math.uwaterloo.ca e-mail: djokovic@uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By applying the Cayley–Dickson process to the division algebra of real octonions, one obtains a 16-dimensional real algebra known as (real) sedenions. We denote this algebra by 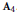${{\text{A}}_{4}}$. It is a flexible quadratic algebra (with unit element 1) but not a division algebra.

We classify the subalgebras of 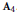${{\text{A}}_{4}}$ up to conjugacy (i.e., up to the action of the automorphism group $G$ of 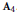${{\text{A}}_{4}}$) with one exception: we leave aside the more complicated case of classifying the quaternion subalgebras. Any nonzero subalgebra contains 1 and we show that there are no proper subalgebras of dimension 5, 7 or > 8. The proper non-division subalgebras have dimensions 3, 6 and 8. We show that in each of these dimensions there is exactly one conjugacy class of such subalgebras. There are infinitely many conjugacy classes of subalgebras in dimensions 2 and 4, but only 4 conjugacy classes in dimension 8.

Keywords

17A4517A3617A20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 4 , 01 December 2006 , pp. 492 - 507
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Baez, J., The octonions. Bull. Amer. Math. Soc. 39(2002), 145–205.Google Scholar
[2] Brown, R. B., On generalized Cayley–Dickson algebras. Pacific J. Math. 20(1967), 415–422.Google Scholar
[3] Chan, K. C., The Sedenions and Its Subalgebras. Masters Thesis, University of Waterloo, 2004.Google Scholar
[4] Eakin, P. and Sathaye, A., On automorphisms and derivations of Cayley–Dickson algebras. J. Algebra 129(1990), 263–278.Google Scholar
[5] Greenberg, M. J. and Harper, J. R., Algebraic Topology, A First Course. Mathematics Lecture Note Series 58, Benjamin/Cummings, Reading, MA, 1981.Google Scholar
[6] Jacobson, N., Composition algebras and their automorphisms. Rend. Circ. Mat. Palermo (2) 7(1958), 1–26.Google Scholar
[7] Kervaire, M., Non-parallelizibility of the n sphere for n > 7. Proc. Nat. Acad. Sci. 44(1958), 280–283.+7.+Proc.+Nat.+Acad.+Sci.+44(1958),+280–283.>Google Scholar
[8] Khalil, S. H. and Yiu, P., The Cayley–Dickson algebras, a theorem of A. Hurwitz, and quaternions. Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 24(1997), 117–169.Google Scholar
[9] Kuwata, S., Born–Infeld Lagrangian using Cayley–Dickson algebras. Internat. J. Modern Phys. A 19(2004), no. 10, 1525–1548.Google Scholar
[10] Löhmus, J., Paal, E., and Sorgsepp, L., Nonassociative Algebras in Physics. Hadronic Press, Palm Harbor, FL, 1994.Google Scholar
[11] Milnor, J. and Bott, R., On the parallelizibility of the spheres. Bull. Amer. Math. Soc. 64(1958), 87–89.Google Scholar
[12] Moreno, G., The zero divisors of the Cayley–Dickson algebras over the real numbers. Bol. Soc. Mat. Mexicana (3) 4(1998), 13–28.Google Scholar
[13] Schafer, R. D., On the algebras formed by the Cayley–Dickson process. Amer. J. Math. 76(1954), 435–446.Google Scholar