Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-25T17:57:19.578Z Has data issue: false hasContentIssue false
  • English
  • Français

C*-Crossed-Products by an Order-Two Automorphism

Published online by Cambridge University Press:  20 November 2018

Man-Duen Choi  and
Frédéric Latrémolière
Man-Duen Choi
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON e-mail: choi@math.toronto.edu
Frédéric Latrémolière
Affiliation:
Department of Mathematics, University of Denver, Denver, CO 80208, USA e-mail: Frederic.Latremoliere@math.du.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe the representation theory of 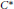${{C}^{*}}$-crossed-products of a unital 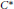${{C}^{*}}$-algebra 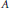$A$ by the cyclic group of order 2. We prove that there are two main types of irreducible representations for the crossed-product: those whose restriction to 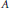$A$ is irreducible and those who are the sum of two unitarily unequivalent representations of 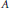$A$. We characterize each class in term of the restriction of the representations to the fixed point 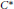${{C}^{*}}$-subalgebra of 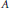$A$. We apply our results to compute the 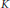$K$-theory of several crossed-products of the free group on two generators.

Keywords

46L5546L80C*-algebraC*-crossed-productfixed pointC*-algebraaction of finite groupsfree groupC*-algebras
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 1 , 01 March 2010 , pp. 37 - 50
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Choi, M.-D. and Latrémolière, F., The C*-algebra of symmetric words in two universal unitaries. arXivmath.OA/0610467.Google Scholar
[2] Cuntz, J., The K-groups for free products of C*-algebras. Proc. Sympos. Pure Math. 38(1982), 81–84.Google Scholar
[3] Rieffel, M., Induced representations of C*-algebras. Advances in Math. 13(1974), 176–257. doi:10.1016/0001-8708(74)90068-1Google Scholar
[4] Rieffel, M., Actions of finite groups on C*-algebras. Math. Scand. 47(1980), 157–176.Google Scholar
[5] Zeller-Meier, G., Produits croisés d’une C*-algèbre par un groupe d’automorphismes. J. Math. Pures Appl. 47(1968), 101–239.Google Scholar