Article contents
C*-Algebras of Infinite Graphs and Cuntz-Krieger Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
The Cuntz-Krieger algebra 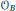 ${{\mathcal{O}}_{B}}$ is defined for an arbitrary, possibly infinite and infinite valued, matrix
${{\mathcal{O}}_{B}}$ is defined for an arbitrary, possibly infinite and infinite valued, matrix 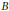 $B$. A graph
$B$. A graph 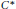 ${{C}^{*}}$-algebra
${{C}^{*}}$-algebra 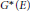 ${{G}^{*}}\left( E \right)$ is introduced for an arbitrary directed graph
${{G}^{*}}\left( E \right)$ is introduced for an arbitrary directed graph 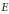 $E$, and is shown to coincide with a previously defined graph algebra
$E$, and is shown to coincide with a previously defined graph algebra 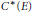 ${{C}^{*}}\left( E \right)$ if each source of
${{C}^{*}}\left( E \right)$ if each source of 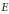 $E$ emits only finitely many edges. Each graph algebra
$E$ emits only finitely many edges. Each graph algebra 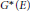 ${{G}^{*}}\left( E \right)$ is isomorphic to the Cuntz-Krieger algebra
${{G}^{*}}\left( E \right)$ is isomorphic to the Cuntz-Krieger algebra 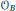 ${{\mathcal{O}}_{B}}$ where
${{\mathcal{O}}_{B}}$ where 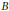 $B$ is the vertex matrix of
$B$ is the vertex matrix of 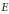 $E$.
$E$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2002
References
- 1
- Cited by




