Article contents
The Bifurcation Diagram of Cubic Polynomial Vector Fields on CP1
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper we give the bifurcation diagram of the family of cubic vector fields 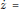 $\dot{z}=$
$\dot{z}=$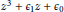 ${{z}^{3}}+{{\epsilon }_{1}}z+{{\epsilon }_{0}}$ for
${{z}^{3}}+{{\epsilon }_{1}}z+{{\epsilon }_{0}}$ for 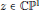 $z\in \mathbb{C}{{\mathbb{P}}^{1}}$, depending on the values of
$z\in \mathbb{C}{{\mathbb{P}}^{1}}$, depending on the values of 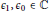 ${{\epsilon }_{1}},{{\epsilon }_{0}}\in \mathbb{C}$. The bifurcation diagram is in
${{\epsilon }_{1}},{{\epsilon }_{0}}\in \mathbb{C}$. The bifurcation diagram is in 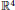 ${{\mathbb{R}}^{^{4}}}$, but its conic structure allows describing it for parameter values in
${{\mathbb{R}}^{^{4}}}$, but its conic structure allows describing it for parameter values in 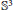 ${{\mathbb{S}}^{3}}$. There are two open simply connected regions of structurally stable vector fields separated by surfaces corresponding to bifurcations of homoclinic connections between two separatrices of the pole at infinity. These branch from the codimension 2 curve of double singular points. We also explain the bifurcation of homoclinic connection in terms of the description of Douady and Sentenac of polynomial vector fields.
${{\mathbb{S}}^{3}}$. There are two open simply connected regions of structurally stable vector fields separated by surfaces corresponding to bifurcations of homoclinic connections between two separatrices of the pole at infinity. These branch from the codimension 2 curve of double singular points. We also explain the bifurcation of homoclinic connection in terms of the description of Douady and Sentenac of polynomial vector fields.
- Type
- Research Article
- Information
- Creative Commons
- © Canadian Mathematical Society 2017 This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 4
- Cited by




