Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jespers, E.
and
Leal, G.
1995.
Degree 1 and 2 representations of nilpotent groups and applications to units of group rings.
Manuscripta Mathematica,
Vol. 86,
Issue. 1,
p.
479.
Parmenter, M. M.
1995.
Conjugates of units in integral group rings.
Communications in Algebra,
Vol. 23,
Issue. 14,
p.
5503.
Jespers, Eric
and
Milies, C.Polcino
1996.
Units of group rings.
Journal of Pure and Applied Algebra,
Vol. 107,
Issue. 2-3,
p.
233.
Li, Yuanlin
1998.
Units OF Z(G × C2).
Quaestiones Mathematicae,
Vol. 21,
Issue. 3-4,
p.
201.
Sehgal, S.K.
2003.
Vol. 3,
Issue. ,
p.
455.
DOOMS, ANN
2006.
UNITARY UNITS IN INTEGRAL GROUP RINGS.
Journal of Algebra and Its Applications,
Vol. 05,
Issue. 01,
p.
43.
LOW, RICHARD M.
2008.
ON THE UNITS OF THE INTEGRAL GROUP RING Z[G × Cp].
Journal of Algebra and Its Applications,
Vol. 07,
Issue. 03,
p.
393.
Bilgin, Tevfik
Kusmus, Omer
and
Low, Richard M.
2016.
A CHARACTERIZATION OF THE UNIT GROUP IN ℤ[T×C2].
Bulletin of the Korean Mathematical Society,
Vol. 53,
Issue. 4,
p.
1105.
Bächle, Andreas
Maheshwary, Sugandha
and
Margolis, Leo
2021.
Abelianization of the unit group of an integral group ring.
Pacific Journal of Mathematics,
Vol. 312,
Issue. 2,
p.
309.
Küsmüş, Ömer
Denizler, İsmail
and
Low, Richard M.
2024.
On the Unit Group of the Integral Group Ring Z(S_3×C_3).
Yüzüncü Yıl Üniversitesi Fen Bilimleri Enstitüsü Dergisi,
Vol. 29,
Issue. 1,
p.
157.
Malik, Sandeep
and
Sharma, R. K.
2024.
Describing the group of units of integral grouprings ℤD8 and ℤD12.
Asian-European Journal of Mathematics,
Vol. 17,
Issue. 01,
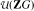 for the two groups G = D12 and G = D8 × C2. In particular, it is shown that in both cases the bicyclic units generate a torsion-free normal complement. It follows that the Bass-cyclic units together with the bicyclic units generate a subgroup of finite index in
for the two groups G = D12 and G = D8 × C2. In particular, it is shown that in both cases the bicyclic units generate a torsion-free normal complement. It follows that the Bass-cyclic units together with the bicyclic units generate a subgroup of finite index in 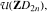 for all n ≥ 3.
for all n ≥ 3.



