Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-01T02:20:32.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Bernstein-Type Inequalities with Bombieri Norm

Published online by Cambridge University Press:  20 November 2018

Franck Beaucoup  and
Catherine Souchon
Franck Beaucoup
Affiliation:
Ecole des Mines de Saint-Etienne, Equipe Mathématiques Appliquées, 158 cours Fauriel, 42023 Saint-Etienne, France, e-mail:beaucoup@emse.fr
Catherine Souchon
Affiliation:
Université Lyon 1, Département de Mathématiques, 69622 Villeurbanne, France, e-mail:souchon@jonas.univ-lyonl.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 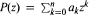is an univariate polynomial with degree n then Bombieri norm of P is defined by

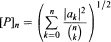
where 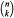denotes the binomial coefficient.

In the present paper we give, under assumptions on the roots of P, optimal Bernsteintype inequalities for the ratio between Bombieri norm of P and that of its derivative P′.

We also give such inequalities for the polar derivatives of P defined by

Keywords

30C1541A17polynomialBernstein inequalityBombieri normrootspolar derivatives
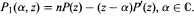
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 2 , 01 June 1996 , pp. 151 - 163
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Beaucoup, F., Estimations quantitatives sur les polynômes liées à la répartition des racines, Thèse de Doctorat, Université Lyon 1, 1994.Google Scholar
2. Beauzamy, B., Bombieri, E., R Enflo and Montgomery, H., Products of polynomials in many variables, J. Number Theory 36(1990), 219–245.Google Scholar
3. Boyd, D. W., Bounds for the height of a factor of a polynomial in terms of Bombieri norms. I. The largest factor, to appear in J. Symbolic Comput.Google Scholar
4. De Bruijn, N., Inequalities concerning polynomials in the complex domain, Proc. Konink. Nederl. Akad. Wetensch. 50(1947), 1265–1272.Google Scholar
5. Durand, A., Relation de Szegö sur la dérivée d'un polynôme, Fifty years of polynomials, Lecture notes in Mathematics, Springer, Berlin 1415(1988).Google Scholar
6. Frot, J.-L., Rang d'un polynôme homogène en plusieurs variables; to appear.Google Scholar
7. Govil, N. K. and Rahman, Q. I., Functions of exponential type not vanishing in a half plane and related polynomials, Trans. Amer. Math. Soc. 137(1969), 501–517.Google Scholar
8. Henrici, P., Applied and computational complex analysis, Wiley Classics Lib. 1(1974).Google Scholar
9. Lax, P. D., Proof of a conjecture of P. Erdôs on the derivative of a polynomial, Bull. Amer. Math. Soc. 50(1944), 509–513.Google Scholar
10. Malik, M. A., On the derivative of a polynomial, J. London Math. Soc. (2) 1(1969), 57–60.Google Scholar
11. Rahman, Q. I., Some inequalities for polynomials and related entire fonctions II, Canad. Math. Bull. 7( 1964), 573–595.Google Scholar
12. Reznick, B., An inequality for products of polynomials, Proc. Amer. Math. Soc. 117(1993), 1063–1073.Google Scholar
13. Zygmund, A., A remark on conjugate series, Proc. London Math. Soc. 34(1932), 392–400.Google Scholar