Article contents
Rings whose Elements are the Sum of a Tripotent and an Element from the Jacobson Radical
Published online by Cambridge University Press: 15 March 2019
Abstract
This paper is about rings 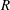 $R$ for which every element is a sum of a tripotent and an element from the Jacobson radical
$R$ for which every element is a sum of a tripotent and an element from the Jacobson radical 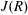 $J(R)$. These rings are called semi-tripotent rings. Examples include Boolean rings, strongly nil-clean rings, strongly 2-nil-clean rings, and semi-boolean rings. Here, many characterizations of semi-tripotent rings are obtained. Necessary and sufficient conditions for a Morita context (respectively, for a group ring of an abelian group or a locally finite nilpotent group) to be semi-tripotent are proved.
$J(R)$. These rings are called semi-tripotent rings. Examples include Boolean rings, strongly nil-clean rings, strongly 2-nil-clean rings, and semi-boolean rings. Here, many characterizations of semi-tripotent rings are obtained. Necessary and sufficient conditions for a Morita context (respectively, for a group ring of an abelian group or a locally finite nilpotent group) to be semi-tripotent are proved.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
References
- 5
- Cited by




