No CrossRef data available.
Article contents
Every symmetric Kubo–Ando connection has the order-determining property
Published online by Cambridge University Press: 11 September 2023
Abstract
In this article, the question of whether the Löwner partial order on the positive cone of an operator algebra is determined by the norm of any arbitrary Kubo–Ando mean is studied. The question was affirmatively answered for certain classes of Kubo–Ando means, yet the general case was left as an open problem. We here give a complete answer to this question, by showing that the norm of every symmetric Kubo–Ando mean is order-determining, i.e., if 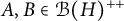 $A,B\in \mathcal B(H)^{++}$ satisfy
$A,B\in \mathcal B(H)^{++}$ satisfy 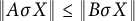 $\Vert A\sigma X\Vert \le \Vert B\sigma X\Vert $ for every
$\Vert A\sigma X\Vert \le \Vert B\sigma X\Vert $ for every 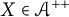 $X\in \mathcal {A}^{{++}}$, where
$X\in \mathcal {A}^{{++}}$, where 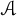 $\mathcal A$ is the C*-subalgebra generated by
$\mathcal A$ is the C*-subalgebra generated by 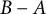 $B-A$ and I, then
$B-A$ and I, then 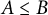 $A\le B$.
$A\le B$.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society





