Research Article
On Outwardly Simple Line Families
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-11
-
- Article
-
- You have access
- Export citation
On The Number of Faces of a Convex Polytope
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-17
-
- Article
-
- You have access
- Export citation
On Covering Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 18-27
-
- Article
-
- You have access
- Export citation
Ideals in Topological Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-45
-
- Article
-
- You have access
- Export citation
Collineations of Affine Moulton Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 46-62
-
- Article
-
- You have access
- Export citation
Completions of Quadrangles in Projective Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-76
-
- Article
-
- You have access
- Export citation
A Note on Cayley Loops
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 77-81
-
- Article
-
- You have access
- Export citation
Traces of a Class Of (0, 1)-Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-93
-
- Article
-
- You have access
- Export citation
Determining a Set from the Cardinalities of its Intersections with Other Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 94-97
-
- Article
-
- You have access
- Export citation
Variation-Diminishing Transformations and General Orthogonal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-107
-
- Article
-
- You have access
- Export citation
From Matrices to Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 108-127
-
- Article
-
- You have access
- Export citation
Counting Coloured Graphs II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 128-135
-
- Article
-
- You have access
- Export citation
Free Lattices Generated by Partially Ordered Sets and Preserving Bounds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-148
-
- Article
-
- You have access
- Export citation
Complemented Banach Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-150
-
- Article
-
- You have access
- Export citation
Sums of the Divisor Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 151-158
-
- Article
-
- You have access
- Export citation
Motions of Matrix Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-165
-
- Article
-
- You have access
- Export citation
A Homomorphism in Exterior Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-168
-
- Article
-
- You have access
- Export citation
Conical Differentiation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 169-190
-
- Article
-
- You have access
- Export citation
Modular Representations of Sn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-203
-
- Article
-
- You have access
- Export citation
Weak Compactness and Separation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-206
-
- Article
-
- You have access
- Export citation

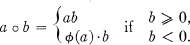

 be the family of orthonormal polynomials associated with a, so that
be the family of orthonormal polynomials associated with a, so that

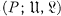 generated by the partially ordered set
generated by the partially ordered set 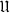 of finite subsets of
of finite subsets of  .
.

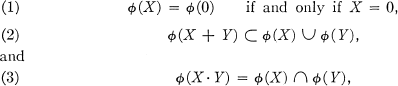
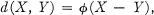
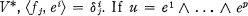 and
and 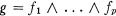 , then the operators *(
, then the operators *(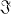 = range of ∊(u) and the sub-algebra
= range of ∊(u) and the sub-algebra 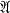 = range of
= range of