Research Article
Sur De Nouvelles Solutions Oscillatoires Des Equations De La Gravitation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-16
-
- Article
-
- You have access
- Export citation
The Coordinate Conditions and the Equations of Motion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-25
-
- Article
-
- You have access
- Export citation
Multiple Quantization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-36
-
- Article
-
- You have access
- Export citation
The Propagation of a Plane Shock into a Quiet Atmosphere
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 37-39
-
- Article
-
- You have access
- Export citation
Corresponding Polyhedra in the Three Spaces of Constant Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-45
-
- Article
-
- You have access
- Export citation
A Simple Bounding Formula for Integrals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 46-52
-
- Article
-
- You have access
- Export citation
Constant Holomorphic Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 53-56
-
- Article
-
- You have access
- Export citation
Harmonic p-Tensors on Normal Hyperbolic Riemannian Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 57-80
-
- Article
-
- You have access
- Export citation
Partitioning an Arithmetic Interval
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
-
- Article
-
- You have access
- Export citation
Proof of a Conjecture of Schoenberg on the Generating Function of a Totally Positive Sequence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-94
-
- Article
-
- You have access
- Export citation
The Boolean Algebra of Regular Open Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-100
-
- Article
-
- You have access
- Export citation
Continuous Solutions of the Functional Equation fn(x) = f(x)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 101-103
-
- Article
-
- You have access
- Export citation
Generating Functions for Bessel and Related Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-106
-
- Article
-
- You have access
- Export citation
On Two-Dimensional Bernstein Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-113
-
- Article
-
- You have access
- Export citation
A Convolution Transform Admitting an Inversion Formula of Integro-Differential Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-117
-
- Article
-
- You have access
- Export citation
Systems of Partial Differential Equations Which Generalize the Heat Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 118-128
-
- Article
-
- You have access
- Export citation
Sur Les Applications Lineaires Faiblement Compactes D'Espaces Du Type C(K)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-173
-
- Article
-
- You have access
- Export citation
Some Multiplicative Functionals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-178
-
- Article
-
- You have access
- Export citation
Integral Functions With Negative Zeros
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 179-184
-
- Article
-
- You have access
- Export citation
On The Number of Symmetry Types of Boolean Functions of n Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-193
-
- Article
-
- You have access
- Export citation

 their conjugates. The subscripts a, b, c, … run from 1 to n and by
their conjugates. The subscripts a, b, c, … run from 1 to n and by  .
.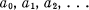
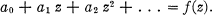

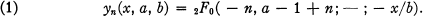



 son dual (espace des mesures de Radon sur
son dual (espace des mesures de Radon sur