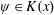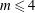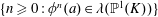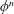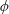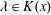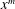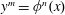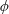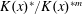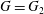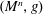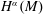Article
Linear Maps Preserving Matrices of Local Spectral Radius Zero at a Fixed Vector
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 749-771
-
- Article
-
- You have access
- Export citation
Powers in Orbits of Rational Functions: Cases of an Arithmetic Dynamical Mordell–Lang Conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 773-817
-
- Article
-
- You have access
- Export citation
The Variety of Two-dimensional Algebras Over an Algebraically Closed Field
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2018, pp. 819-842
-
- Article
-
- You have access
- Export citation
The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 843-889
-
- Article
-
- You have access
- Export citation
Cohomological Approach to Class Field Theory in Arithmetic Topology
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 891-935
-
- Article
-
- You have access
- Export citation
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 937-982
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 983-995
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
CJM volume 71 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 July 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
CJM volume 71 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 July 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation