Research Article
Essentially Convexoid Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-274
-
- Article
-
- You have access
- Export citation
σ4-Actions On Homotopy Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 275-281
-
- Article
-
- You have access
- Export citation
Diamond Principles, Ideals and the Normal Moore Space Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-296
-
- Article
-
- You have access
- Export citation
Absolute Approximate Retracts and AR-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-301
-
- Article
-
- You have access
- Export citation
Algebraic Homotopy Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 302-319
-
- Article
-
- You have access
- Export citation
Irregularity of the Rate of Decrease of Sequences of Powers in the Volterra Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-324
-
- Article
-
- You have access
- Export citation
Localization and Completion at Primes Generated by Normalizing Sequences in Right Noetherian Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 325-346
-
- Article
-
- You have access
- Export citation
Expansions of Arbitrary Analytic Functions in Series of Exponentials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-356
-
- Article
-
- You have access
- Export citation
Strong Convergence of Pramarts in Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 357-361
-
- Article
-
- You have access
- Export citation
Birkhoff Interpolation at the nth Roots of Unity: Convergence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 362-371
-
- Article
-
- You have access
- Export citation
Wallman Compactification and Representation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 372-380
-
- Article
-
- You have access
- Export citation
Signatures of Covering Links
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-394
-
- Article
-
- You have access
- Export citation
Rankings and Ranking Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-399
-
- Article
-
- You have access
- Export citation
An Essential Integral Domain with a Non-Essential Localization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-403
-
- Article
-
- You have access
- Export citation
On the Structure of Finitely Presented Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 404-411
-
- Article
-
- You have access
- Export citation
Nilpotent Partition-Inducing Automorphism Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-420
-
- Article
-
- You have access
- Export citation
On the Number and Distribution of Simultaneous Solutions to Diagonal Congruences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 421-436
-
- Article
-
- You have access
- Export citation
Uniqueness of Certain Spherical Codes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 437-449
-
- Article
-
- You have access
- Export citation
Completely Regular Mappings and Homogeneous, Aposyndetic Continua
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 450-453
-
- Article
-
- You have access
- Export citation
Lying-Over Pairs of Commutative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 454-475
-
- Article
-
- You have access
- Export citation

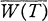 of its numerical range
of its numerical range 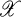 is a topological space then a sequence (
is a topological space then a sequence (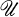 and
and 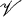 such that
such that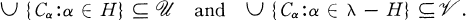
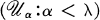 of pairwise disjoint open sets such that
of pairwise disjoint open sets such that 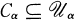 for each
for each 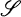 is the category of simplicial sets and
is the category of simplicial sets and 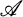 is the category of
is the category of 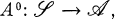
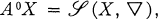
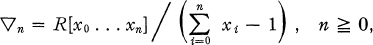
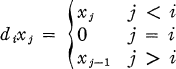
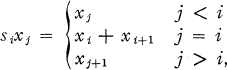
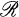 possesses bounded approximate identities then for every sequence (
possesses bounded approximate identities then for every sequence (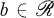 such that
such that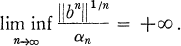
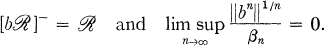
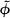 of
of 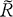 , the complement of
, the complement of 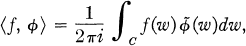
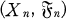 be an adapted sequence on the probability space
be an adapted sequence on the probability space 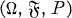 We denote by
We denote by 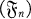 .
. 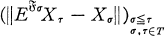
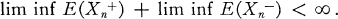
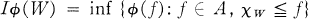
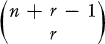 . Of course only some strict orderings of this set of results will be feasible in that there are criteria which a final ranking should satisfy. For example, (1, 1, …, 1) should clearly be ranked first in any feasible ranking.
. Of course only some strict orderings of this set of results will be feasible in that there are criteria which a final ranking should satisfy. For example, (1, 1, …, 1) should clearly be ranked first in any feasible ranking.