Research Article
IP-Sets on the Circle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-589
-
- Article
-
- You have access
- Export citation
The Failure of Cancellation Laws for Equidecomposability Types
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 590-606
-
- Article
-
- You have access
- Export citation
Sur Une Formule de Ramanujan-Bailey
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 607-618
-
- Article
-
- You have access
- Export citation
Extremal Problems for the Classes SR-p and TR-p
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 619-645
-
- Article
-
- You have access
- Export citation
Restricted Determinantal Homomorphisms and Locally Free Class Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 646-658
-
- Article
-
- You have access
- Export citation
Two Families of Associated Wilson Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 659-695
-
- Article
-
- You have access
- Export citation
Functional Equations, Distributions and Approximate Identities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-708
-
- Article
-
- You have access
- Export citation
Analytic Isomorphisms of Transformation Group C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 709-730
-
- Article
-
- You have access
- Export citation
Simply Connected Limits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 731-746
-
- Article
-
- You have access
- Export citation
Isomorphism Classes of Graph Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-761
-
- Article
-
- You have access
- Export citation

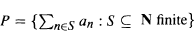 for a certain sequence
for a certain sequence 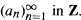 The main questions studied here are : (1) Under what conditions on (
The main questions studied here are : (1) Under what conditions on (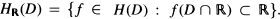 Furthermore, denote by
Furthermore, denote by