Research Article
Injectives and Projectives in Term Finite Varieties of Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 769-775
-
- Article
-
- You have access
- Export citation
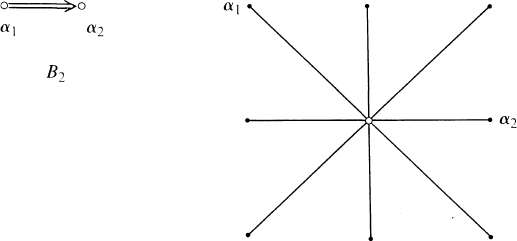
Alternating 3-Forms and Exceptional Simple Lie Groups of Type G2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 776-806
-
- Article
-
- You have access
- Export citation
Normal, Locally Compact, Boundedly Metacompact Spaces are Paracompact: an Application of Pixley-Roy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 807-823
-
- Article
-
- You have access
- Export citation
Two Boolean Algebras with Extreme Cellular and Compactness Properties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 824-838
-
- Article
-
- You have access
- Export citation
Global Positive Solutions of Semilinear Elliptic Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 839-861
-
- Article
-
- You have access
- Export citation
On a Generalized Fundamental Equation of Information
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 862-872
-
- Article
-
- You have access
- Export citation
On Difference Operators and their Factorization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 873-897
-
- Article
-
- You have access
- Export citation
λ-Mappings Between Representation Rings of Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 898-960
-
- Article
-
- You have access
- Export citation

 is
is  and whenever
and whenever  and
and 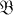 into
into 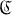 and
and 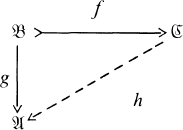
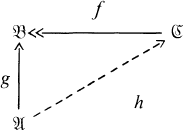

 of type
of type 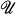 of
of 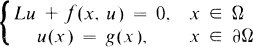
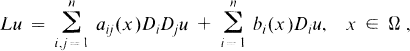
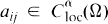 ,
, 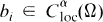 , and (
, and (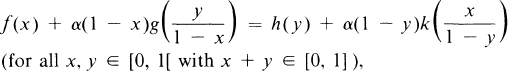
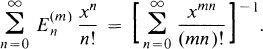
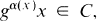
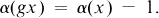
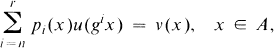
 is a complex simple Lie algebra of type
is a complex simple Lie algebra of type 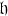 be a Cartan subalgebra of
be a Cartan subalgebra of