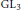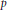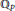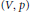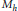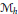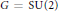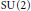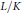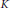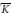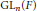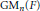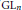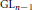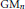Research Article
Ramanujan Type Buildings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1121-1148
-
- Article
-
- You have access
- Export citation
Canonical Resolution of a Quasi-ordinary Surface Singularity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1149-1163
-
- Article
-
- You have access
- Export citation
Perforated Ordered K0-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1164-1191
-
- Article
-
- You have access
- Export citation
Orbital Integrals on p-Adic Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1192-1220
-
- Article
-
- You have access
- Export citation
Nest Representations of TAF Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1221-1234
-
- Article
-
- You have access
- Export citation
Representations with Weighted Frames and Framed Parabolic Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1235-1268
-
- Article
-
- You have access
- Export citation
Well Ramified Extensions of Complete Discrete Valuation Fields with Applications to the Kato Conductor
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1269-1309
-
- Article
-
- You have access
- Export citation
On the Homology of GLn and Higher Pre-Bloch Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1310-1338
-
- Article
-
- You have access
- Export citation
Index of Volume 52
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1339-1343
-
- Article
-
- You have access
- Export citation