Hostname: page-component-7bb8b95d7b-dtkg6 Total loading time: 0 Render date: 2024-09-13T04:01:09.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Zariski Hyperplane Section Theorem for Grassmannian Varieties

Published online by Cambridge University Press:  20 November 2018

Ichiro Shimada
Ichiro Shimada*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan, email: shimada@math.sci.hokudai.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 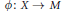$\phi :\,X\,\to \,M$ be a morphism from a smooth irreducible complex quasi-projective variety 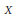$X$ to a Grassmannian variety 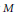$M$ such that the image is of dimension ≥ 2. Let 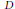$D$ be a reduced hypersurface in 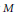$M$, and 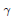$\gamma $ a general linear automorphism of 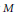$M$. We show that, under a certain differential-geometric condition on 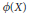$\phi (X)$ and 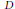$D$, the fundamental group 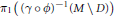${{\text{ }\!\!\pi\!\!\text{ }}_{1}}\left( {{\left( \gamma \,o\,\phi \right)}^{-1}}\,\left( M\,\backslash \,D \right) \right)$ is isomorphic to a central extension of 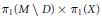${{\pi }_{1}}\left( M\,\backslash \,D \right)\,\,\times \,{{\pi }_{1}}\left( X \right)$ by the cokernel of 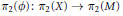${{\pi }_{2}}\left( \phi \right)\,:\,{{\pi }_{2}}\left( X \right)\,\to {{\pi }_{2}}\left( M \right)$.

Keywords

14F3514M15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 157 - 180
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Catanese, F. and Tovena, F., Vector bundles, linear systems and extensions of π1 . In: Complex algebraic varieties (Bayreuth, 1990), Lecture Notes in Math. 1507, Springer, Berlin, 1992, 51–70.Google Scholar
[2] Debarre, Olivier, Sur un théorème de connexité de Mumford pour les espaces homogènes. Manuscripta Math. (4) 89 (1996), 407–425.Google Scholar
[3] Fulton, William and Lazarsfeld, Robert, Connectivity and its applications in algebraic geometry. In: Algebraic geometry (Chicago, Ill., 1980), Lecture Notes in Math. 862, Springer, Berlin, 1981, 26–92.Google Scholar
[4] Gel′ofand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants. Birkhäuser Boston Inc., Boston, MA, 1994.Google Scholar
[5] Goresky, Mark and MacPherson, Robert, Stratified Morse theory. Springer-Verlag, Berlin, 1988.Google Scholar
[6] Hamm, Helmut A. and Dung Tráng, Lê, Un théorème de Zariski du type de Lefschetz. Ann. Sci. E´ cole Norm. Sup. (4) 6 (1973), 317–355.Google Scholar
[7] Harris, Joe, Algebraic geometry. A first course. Corrected reprint of the 1992 original. Graduate Texts in Math. 133, Springer-Verlag, New York, 1995.Google Scholar
[8] Shimada, Ichiro, On the Zariski-van Kampen theorem. Canad. J. Math, 55 (2003), 133–156.Google Scholar
[9] Zariski, Oscar, On the Poincaré group of rational plane curves. Amer. J. Math. 58 (1936), 607–619; Collected Papers, Volume III. The MIT Press, Cambridge, Mass.-London, 266–278.Google Scholar