Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T13:16:00.350Z Has data issue: false hasContentIssue false
  • English
  • Français

Weingarten Type Surfaces in ℍ2 × ℝ and 𝕊2 × ℝ

Published online by Cambridge University Press:  20 November 2018

Abigail Folha  and
Carlos Peñafiel
Abigail Folha
Affiliation:
Universidade Federal Fluminense, Instituto de Matemática e Estatística, Departamento de Geometria, Niterói, RJ-Brasil e-mail: abigailfolha@vm.uff.br
Carlos Peñafiel
Affiliation:
Universidade Federal de Rio de Janeiro, Instituto de Matemática e Estatística, Departamento de Métodos Matemáticos, Rio de Janeiro, RJ-Brasil e-mail: penafiel@im.ufrj.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we study complete surfaces $\sum $, isometrically immersed in the product spaces 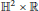${{\mathbb{H}}^{2}}\,\times \,\mathbb{R}$ or 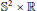${{\mathbb{S}}^{2\,}}\times \,\mathbb{R}$ having positive extrinsic curvature 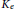${{K}_{e}}$. Let 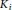${{K}_{i}}$ denote the intrinsic curvature of $\sum $. Assume that the equation 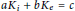$a{{K}_{i\,}}\,+\,b{{K}_{e\,}}\,=\,c$ holds for some real constants 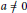$a\,\ne \,0$, 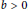$b\,>\,0$, and $c$. The main result of this article states that when such a surface is a topological sphere, it is rotational.

Keywords

53C4253C50Weingarten surfaceextrinsic curvatureintrinsic curvatureheight estimaterotational Weingarten surface
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 6 , 01 December 2017 , pp. 1292 - 1311
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Abresch, U. and Rosenberg, H., A Hopf differential for constant mean curvature surfaces in and . Acta Math. 193(2004), 141–174.http://dx.doi.org/10.1007/BF02392562 Google Scholar
[2] Abresch, U., Generalized Hopf differentials Mat. Contemp. 28(2005), 1–28.Google Scholar
[3] Aledo, A., Espinar, J. M., and Gálvez, J. A., Complete surfaces of constant curvature in and . Calc. Var. Partial Differential Equations 29(2007), no. 3, 347–363.http://dx.doi.org/10.1007/s00526-006-0067-4 Google Scholar
[4] Aledo, A., Surfaces with Constant Curvature in . Height Estimates and Representation. Bull. Braz. Math. Soc, 38, 2007, no. 533–554. http://dx.doi.org/10.1007/s00574-007-0059-9 Google Scholar
[5] Daniel, B., Isometric immersions into 3-dimensional homogeneous manifolds. Comment. Math. Helv. 82(2007), 87–131.http://dx.doi.Org/10.4171/CMH/86 Google Scholar
[6] Dillen, F., Fastenakels, J., Van der Veken, J., and Vrancken, L., Constant angle surfaces in . Monatsh. Math. 152(2007), 89–96.http://dx.doi.org/10.1007/s00605-007-0461-9 Google Scholar
[7] Dillen, F. and Munteanu, M., Constant angle surfaces in . Bulletin Braz. Math. Soc. 40(2009), 85–97.http://dx.doi.org/10.1007/s00574-009-0004-1 Google Scholar
[8] Espinar, J. M., Gálvez, J. A., and Rosenberg, H., Complete surfaces with positive extrinsic curvature in product spaces. Comment. Math. Helv. 84(2009), 351–386. http://dx.doi.org/10.4171/CMH/165 Google Scholar
[9] Espinar, J. M. and Rosenberg, H., When strictly locally convex hypersurfaces are embedded. Math. Z. 271(2012), no. 3-4,1075–1090.http://dx.doi.org/10.1007/s00209-011-0904-9 Google Scholar
[10] Hopf, H., Differential geometry in the large. Lecture Notes in Mathematics, 1000. Springer-Velarg, Berlin, 1983.Google Scholar
[11] Jost, J., Two-dimensional geometric variational problems. John Wiley & Sons, Chichester, MA, 1991.Google Scholar
[12] Milnor, T. K., Harmonic maps and classical surface theory in Minkowski 3-space. Trans. Amer. Math. Soc. 280(1983), 161–185.Google Scholar
[13] Nelli, B.and Rosenberg, H., Simply connected constant mean curvature surfaces in . Michigan Math. J. 54(2006), 537–543.http://dx.doi.org/10.1307/mmj71163789914 Google Scholar