Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-17T09:32:46.520Z Has data issue: false hasContentIssue false
  • English
  • Français

The Structure of Stable Components

Published online by Cambridge University Press:  20 November 2018

Yingbo Zhang  and
T. Lang
Yingbo Zhang
Affiliation:
Department of Mathematics Beijing Normal University Beijing, China100875
T. Lang
Affiliation:
Department of Mathematics Beijing Normal University Beijing, China100875
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

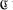Let A be an artin algebra. Let ( be a component of the stable Auslander- Reiten quiver of A. If 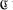is periodic, then the structure of G is known. Here, we are going to consider the case when 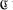is non-periodic: we will show that 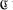is isomorphic to Z 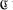with 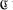a valued quiver. In particular, there is no cyclic path in .

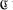Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 3 , 01 June 1991 , pp. 652 - 672
Copyright
Copyright © Canadian Mathematical Society 1991

References

[A] Auslander, M., Applications of morphisms determined by objects. Proc. Conf. on Representation Theory. Philadelphia (1976), Marcel Dekker (1978), 245–327.Google Scholar
[B] Berge, C., Graphs and hypergraphs. North-Holland Publishing Company, 1973.Google Scholar
[BG] Bongartz, K. and Gabriel, P., Covering spaces in representation theory, Invent. Math. 65(1982), 331–378.Google Scholar
[BS] Bautista, R. and Smal, S.O.ø, Nonexistent cycles, Comm. Alg. 11(1983), 1755–1767.Google Scholar
[BR] R, M.C.. Butler and Ringel, C.M., AR-sequences with few middle terms and applications to string algebras,, Comm. Alg. 15(1987), 145–179.Google Scholar
[D] Dicks, W., Groups, trees and projective modules, LNM 790(1980).Google Scholar
[GZ] Gabriel, P. and Zisman, M., Calculus of fractions and homology theory, Erg. Math. 35, Berlin-Heildelberg- New York, Springer, 1967.Google Scholar
[HPR1 Happel, D., Preiser, U. and Ringel, C.M., Vinberg's characterization of Dynkin diagrams using subadditive function with application to DTr-periodic modules, LNM 832(1979), 280–294.Google Scholar
[Re] Reidemeister, K., Einfuhrung in die kombinatorische Topologie. Reprint, Chelsea Publishing Company, New York, N.Y., 1950.Google Scholar
[Ri] Riedtmann, Chr., Algebren, Darstellungsköcher,Überlagerungen und zuriick, Comm. Math. Helv. 55 (1980), 199–224.Google Scholar
[R] Ringel, C.M., Tame algebras and integral quadratic forms, . Springer LNM 1099(1984).Google Scholar
[S] Spanier, E.H., Algebraic Topology. McGraw Hill Book Company, 1966.Google Scholar