Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-12T14:20:43.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Rigidity Results Related to Monge–Ampère Functions

Published online by Cambridge University Press:  20 November 2018

Robert L. Jerrard
Robert L. Jerrard*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, e-mail: rjerrard@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

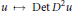The space of Monge–Ampère functions, introduced by J. H. G. Fu, is a space of rather rough functions in which the map $u\,\mapsto \,\text{Det}\,{{\text{D}}^{2}}u$ is well defined and weakly continuous with respect to a natural notion of weak convergence. We prove a rigidity theorem for Lagrangian integral currents that allows us to extend the original definition of Monge–Ampère functions. 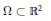We also prove that if a Monge–Ampère function $u$ on a bounded set $\Omega \,\subset \,{{\mathbb{R}}^{2}}$ satisfies the equation 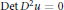$\text{Det}\,{{D}^{2}}u\,=\,0$ in a particular weak sense, then the graph of $u$ is a developable surface, and moreover $u$ enjoys somewhat better regularity properties than an arbitrary Monge–Ampère function of 2 variables.

Keywords

49Q1553C24
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 2 , 01 April 2010 , pp. 320 - 354
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Ambrosio, L., Fusco, N., and Pallara, D., Functions of Bounded Variation and Free Discontinuity Problems. The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[2] Bernig, A., Support functions, projections and Minkowski addition of Legendrian cycles. Indiana Univ. Math. J. 55(2006), no. 2, 443–464. doi:10.1512/iumj.2006.55.2684Google Scholar
[3] Bernig, A. and L. Bröcker, Lipschitz-Killing invariants. Math. Nachr. 245(2002), 5–25. doi:10.1002/1522-2616(200211)245:1h5::AID-MANA5i3.0.CO;2-EGoogle Scholar
[4] Cohen-Steiner, D. and Morvan, J. M., Second fundamental measure of geometric sets and local approximation of curvatures. J. Differential Geom. 74(2006), no. 3, 363–394.Google Scholar
[5] Federer, H., Geometric Measure Theory. Die Grundlehren des mathematischen Wissenschaften 153. Springer-Verlag, New York, 1969.Google Scholar
[6] Fonseca, I. and Maly, J., From Jacobian to Hessian: distributional form and relaxation. Riv. Mat. Univ. Parma 4*(2005), 45–74.Google Scholar
[7] Fu, J. H. G., Monge–Ampère functions. I. Indiana Univ. Math. J. 38(1989), no. 3, 745–771. doi:10.1512/iumj.1989.38.38035Google Scholar
[8] Fu, J. H. G., Monge–Ampère functions. II. Indiana Univ. Math. J. 38(1989), no. 3, 773–789. doi:10.1512/iumj.1989.38.38035Google Scholar
[9] Fu, J. H. G., Curvature measures of subanalytic sets. Amer. J. Math. 116(1994), no. 4, 819–880. doi:10.2307/2375003Google Scholar
[10] Giaquinta, M., Modica, G., and Soucek, J., Cartesian Currents in the Calculus of Variations I, II. Ergebnisse der Mathematik und ihrer Grenzgebiete 37, 38. Springer-Verlag, Berlin, 1998.Google Scholar
[11] Hartman, P. and Nirenberg, L., On spherical image maps whose Jacobians do not change sign. Amer. J. Math. 81(1959), 901–920. doi:10.2307/2372995Google Scholar
[12] Iwaniec, T.. On the concept of the weak Jacobian and Hessian. In: Papers on Analysis. Rep. Univ. Jyväkylä Dep. Math. Stat. 83. University Jyväkylä, 2001, pp. 181–205.Google Scholar
[13] Jerrard, R. L., Some remarks on Monge–Ampère functions. In: Singularities in PDE and the Calculus of Variations. CR M Proc. Lecture Notes 44. American Mathematical Society, Providence, RI, 2008, pp. 89–112.Google Scholar
[14] Jerrard, R. L. and N. Jung. Strict convergence and minimal liftings in BV. Proc. Roy. Soc. Edinburgh Sect. A 134(2004), no. 6, 1163–1176. doi:10.1017/S0308210500003681Google Scholar
[15] Kirchheim, B., Geometry and Rigidity of Microstructures. Habilitation Thesis, Leipzig, 2001.Google Scholar
[16] Pakzad, M. R., On the Sobolev space of isometric immersions. J. Differential Geom. 66(2004), no. 1, 47–69.Google Scholar
[17] Pogorelov, A. V., Vneshnyaya geometriya vypuklykh poverkhnosteı. [The extrinsic geometry of convex surfaces] Izdat. “Nauka”, Moscow 1969.Google Scholar
[18] Rataj, C. and M. Zähle, Normal cycles of Lipschitz manifolds by approximation with parallel sets. Differential Geom. Appl. 19(2003), no. 1, 113–126. doi:10.1016/S0926-2245(03)00020-2Google Scholar
[19] Solomon, B., A new proof of the closure theorem for integral currents. Indiana Univ. Math. J. 33(1984), no. 3, 393–418. doi:10.1512/iumj.1984.33.33022Google Scholar
[20] B.White, Rectifiablity of flat chains. Ann. of Math. 150(1999), no. 1, 165–184. doi:10.2307/121100Google Scholar