Hostname: page-component-84b7d79bbc-g7rbq Total loading time: 0 Render date: 2024-07-25T11:47:07.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Selmer Groups of Elliptic Curves with Complex Multiplication

Published online by Cambridge University Press:  20 November 2018

A. Saikia
A. Saikia*
Affiliation:
McGill University, Montreal, Quebec, H3A 2K6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose 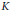$K$ is an imaginary quadratic field and 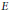$E$ is an elliptic curve over a number field 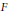$F$ with complex multiplication by the ring of integers in 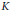$K$. Let 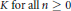$p$ be a rational prime that splits as 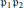${{\mathfrak{p}}_{1}}{{\mathfrak{p}}_{2}}$ in 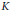$K$. Let 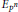${{E}_{{{p}^{n}}}}$ denote the 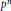${{p}^{n}}$-division points on 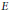$E$. Assume that 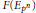$F\left( {{E}_{{{p}^{n}}}} \right)$ is abelian over 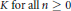$K\,\text{for}\,\text{all}\,n\,\ge \,0$. This paper proves that the Pontrjagin dual of the 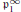$\mathfrak{p}_{1}^{\infty }$-Selmer group of 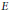$E$ over $F\left( {{E}_{{{p}^{\infty }}}} \right)$ is a finitely generated free 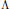$\wedge $-module, where 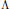$\wedge $ is the Iwasawa algebra of 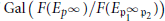$\text{Gal}\left( F\left( {{E}_{{{p}^{\infty }}}} \right)/F\left( E\mathfrak{p}_{1}^{\infty }{{\mathfrak{p}}_{2}} \right) \right)$ . It also gives a simple formula for the rank of the Pontrjagin dual as a 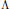$\wedge $-module.

Keywords

11R2311G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 1 , 01 February 2004 , pp. 194 - 208
Copyright
Copyright © Canadian Mathematical Society 2004

References

[C-G] Coates, J. and Greenberg, R., Kummer Theory for abelian varieties over local fields. Invent. Math. 124(1996), 129–174.Google Scholar
[C-H 1] Coates, J. and Howson, S., Euler Characteristics and Elliptic Curves. Proc. Nat. Acad. Sci. U.S.A. (21) 94(1997), 11115–11117.Google Scholar
[C-H 2] Coates, J. and Howson, S., Euler Characteristics and Elliptic Curves II. J. Math. Soc. Japan (1) 53(2001), 175–235.Google Scholar
[C-S] Coates, J. and Sujatha, R., Galois Cohomology of Elliptic Curves. Tata Institute of Fundamental Research Lectures on Mathematics, 2000.Google Scholar
[Gi 1] Gillard, R., Transformation de Mellin-Leopoldt des fonctions elliptiques. J. Number Theory (3) 25(1987), 379–393.Google Scholar
[Gi 2] Gillard, R., Fonctions L p-adiques des corps quadratiques imaginaires et de leurs extensions abeliennes. J. Reine AngewMath. 358(1985), 76–91.Google Scholar
[Gr 1] Greenberg, R., On the structure of certain Galois groups. Invent. Math. 72(1978), 85–99.Google Scholar
[Gr 2] Greenberg, R., Iwasawa theory for elliptic curves. Arithmetic theory of elliptic curves, Cetraro, 1997, Springer-Verlag, 51–144.Google Scholar
[H] Howson, S., Euler characteristics as invariants of Iwasawa modules. preprint.Google Scholar
[H-M] Hachimori, Y. and Matsuno, K., An Analogue of Kida's Formula for the Selmer Groups of Elliptic Curves. J. Algebraic Geom. (3) 8(1999), 581–601.Google Scholar
[H-S] Hochschild, G. and Serre, J. P., Cohomology of group extensions. Trans. Amer.Math. Soc. (1953), 110–134.Google Scholar
[La] Lang, S., Cyclotomic Fields. Springer-Verlag, 1978.Google Scholar
[Mi] Milne, J. S., Arithmetic Duality Theorems. Academic Press, 1986.Google Scholar
[N-S-W] Neukrich, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields. Springer, 1999.Google Scholar
[P-R 1] Perrin-Riou, B., Arithmetique des courbes elliptiques et theórie d'Iwasawa. Mém. Soc. Math. Fr. 17(1984).Google Scholar
[P-R 2] Perrin-Riou, B., Fonctions L p-adiques, theórie d'Iwasawa et points de Heegner. Bull. Soc. Math. France 115(1987), 399–456.Google Scholar
[Se] Serre, J. P., Galois Cohomology. Springer-Verlag, 1997.Google Scholar