Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-11T16:21:38.526Z Has data issue: false hasContentIssue false
  • English
  • Français

The Poisson Integral of a Singular Measure

Published online by Cambridge University Press:  20 November 2018

Patrick Ahern
Patrick Ahern*
Affiliation:
University of Wisconsin — Madison, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let σ be a finite positive singular Borel measure defined on Euclidean space RN. For w ∈ RN and y > 0, its Poisson integral is defined by the formula

where CN is chosen so that

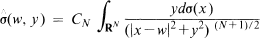
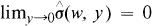Since σ is singular, almost everywhere with respect to Lebesgue measure on RN. On the other hand, 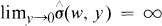almost everywhere dσ. It follows that for all sufficiently small y,

is a non-empty open subset of RN. If σ has compact support then |Ey| → 0 as y → 0, where |Ey| denotes the Lebesgue measure of Ey. In this paper we give a lower bound on the rate at which |Ey| may go to zero. The lower bound depends on the smoothness of the measure; the smoother the measure, the more slowly |Ey| may approach 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 4 , 01 August 1983 , pp. 735 - 749
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Ahern, P., The mean modulus and the derivative of an inner junction, Indiana University Mathematics Journal 28 (1979), 311–347.Google Scholar
2. Ahern, P. and Clark, D., In inner functions with BP derivative, Michigan Mathematics Journal 23 (1976), 107–118.Google Scholar
3. Besicovitch, A., A general form of the covering principle and relative differentiation of additive functions, Proc. Cambridge Philos. Soc. 41 (1945), 103–110.Google Scholar
4. Gluchoff, A, The mean modulus of a Blaschke product, Thesis, University of Wisconsin (1981).Google Scholar
5. Hardy, G., Littlewood, J. and Polya, G., Inequalities (Cambridge, 1934).Google Scholar
6. Jevtić, M., Sur la derivée de la fonction atomique, C. R. Acad. Se. Paris 292 (1981), 201–203.Google Scholar
7. Kahane, J. -P. and Salem, R., Ensembles parfait et séries trigonometrique (Hermann, 1963).Google Scholar
8. Rudin, W., Real and complex analysis, 2nd Ed. (McGraw-Hill, New York, 1974).Google Scholar
9. Walter, W., A counterexample in connection with Egorov's theorem, American Math. Monthly 84 (1977), 118–119.Google Scholar