Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-24T13:06:48.766Z Has data issue: false hasContentIssue false
  • English
  • Français

p-adic and Motivic Measure on Artin n-stacks

Published online by Cambridge University Press:  20 November 2018

Chetan Balwe
Chetan Balwe*
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Mumbai 400005, India. e-mail: cbalwe@math.tifr.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define a notion of 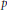$p$-adic measure on Artin $n$-stacks that are of strongly finite type over the ring of 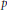$p$-adic integers. 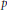$p$-adic measure on schemes can be evaluated by counting points on the reduction of the scheme modulo 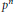${{p}^{n}}$. We show that an analogous construction works in the case of Artin stacks as well if we count the points using the counting measure defined by Toën. As a consequence, we obtain the result that the Poincaré and Serre series of such stacks are rational functions, thus extending Denef's result for varieties. Finally, using motivic integration we show that as 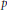$p$ varies, the rationality of the Serre series of an Artin stack defined over the integers is uniform with respect to 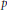$p$.

Keywords

14E1814A20p-adic integrationmotivic integrationArtin stacks
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 6 , 01 December 2015 , pp. 1219 - 1246
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Balwe, C. T., Geometric motivic integration on Artin n-stacks. Ph.D. thesis, University of Pittsburgh, 2008.http://gradworks.umi.com/33/35/3335718.html Google Scholar
[2] Bosch, S., Lütkebohmert, W., and Raynaud, M., Néron models. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 21, Springer-Verlag, Berlin, 1990.Google Scholar
[3] Borger, J., The basic geometry of Witt vectors, I: The affine case. Algebra Number Theory 5(2011), no. 2, 231–285.http://dx.doi.org/10.2140/ant.2011.5.231 Google Scholar
[4] Bourbaki, N., Alégbre commutative. Elments de Math., Hermann, Paris. (1961–65).Google Scholar
[5] Cluckers, R. and Loeser, F., Constructible motivic functions and motivic integration. Invent. Math. 173(2008), no. 1, 23–121.http://dx.doi.org/10.1007/s00222-008-0114-1 Google Scholar
[6] Cluckers, R. and Loeser, F., Constructible exponential functions, motivic Fourier transform and transfer principle. Ann. Of Math. (2) 171(2010), no. 2, 1011–1065.http://dx.doi.org/10.4007/annals.2010.171.1011 Google Scholar
[7] Deligne, P., Cohomologie l-adique et fonctions L (SGA 5), Lecture Notes in Math. 589, Springer-Verlag, Berlin-New York, 1977.Google Scholar
[8] Denef, J., The rationality of the Poincaré series associated to the p-adic points on a variety. Invent. Math. 77(1984), no. 1, 1–23.http://dx.doi.org/10.1007/BF01389133 Google Scholar
[9] Denef, J., and Loeser, F., Definable sets, motives and p-adic integrals. J. Amer. Math. Soc. 14(2001), no. 2, 429–469 (electronic).http://dx.doi.org/10.1090/S0894-0347-00-00360-X Google Scholar
[10] Dugger, D., Hollander, S., and Isaksen, D., Hypercovers and simplicial presheaves. Math. Proc. Cambridge Philos. Soc. 136(2004), no. 1, 9–51.http://dx.doi.org/10.1017/S0305004103007175 Google Scholar
[11] Greenberg, M., Schemata over local rings. Ann. of Math. (2) 73(1961), 624–648.http://dx.doi.org/10.2307/1970321 Google Scholar
[12] Hrushovski, E., Martin, B., Rideau, S., and Cluckers, R., Definable equivalence relations and zeta functions of groups. arxiv:math/0701011.Google Scholar
[13] Illusie, L., Complexe de de Rham-Witt et cohomologie cristalline. Ann. Sci.École Norm. Sup. (4)(1979), no. 4, 501–661.Google Scholar
[14] Knutson, D., Algebraic spaces. Lecture Notes in Mathematics, 203, Springer-Verlag, Berlin-New York, 1971.Google Scholar
[15] Laumon, G. and Moret-Bailly, L., Champs algébriques. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, 39, Springer-Verlag, Berlin, 2000.Google Scholar
[16] Looijenga, E., Motivic measures. Séminaire Bourbaki, 1999/2000, Astérisque 276(2002), 267–297.Google Scholar
[17] Oesterlé, J., Réduction modulo pn des sous-ensembles analytiques fermés de ℤN p. Invent. Math. 66(1982), no. 2, 325–341. http://dx.doi.org/10.1007/BF01389398 Google Scholar
[18] Serre, J.-P., Local fields. Graduate Texts in Mathematics, 67, Springer-Verlag, New York-Berlin, 1979.Google Scholar
[19] Serre, J.-P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 323–401.Google Scholar
[20] Toën, B., Grothendieck rings of Artin n-stacks. arxiv:math/0509098v3[math.AG].Google Scholar
[21] Toën, B. and Vezzosi, G., Homotopical algebraic geometry I: Topos theory. Adv. Math. 193(2005), no. 2, 257–372. http://dx.doi.org/10.1016/j.aim.2004.05.004 Google Scholar
[22] Toën, B. and Vezzosi, G., Homotopical algebraic geometry. II. Geometric stacks and applications. Mem. Amer. Math. Soc. 193(2008), no. 902.Google Scholar