Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-19T05:21:57.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Operators which Factor through Convex Banach Lattices

Published online by Cambridge University Press:  20 November 2018

Shlomo Reisner
Shlomo Reisner*
Affiliation:
Texas A & M University, College Station, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate here classes of operators T between Banach spaces E and F, which have factorization of the form

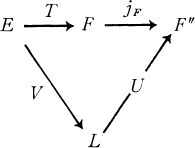
where L is a Banach lattice, V is a p-convex operator, U is a q-concave operator (definitions below) and jF is the cannonical embedding of F in F”. We show that for fixed p, q this class forms a perfect normed ideal of operators Mp, q, generalizing the ideal Ip,q of [5]. We prove (Proposition 5) that Mp, q may be characterized by factorization through p-convex and q-concave Banach lattices. We use this fact together with a variant of the complex interpolation method introduced in [1], to show that an operator which belongs to Mp, q may be factored through a Banach lattice with modulus of uniform convexity (uniform smoothness) of power type arbitrarily close to q (to p). This last result yields similar geometric properties in subspaces of spaces having G.L. – l.u.st.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1482 - 1500
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Calderon, A. P., Intermediate spaces and interpolation, the complex method, Studia Math. 24 (1964), 113–190.Google Scholar
2. Figiel, T., Uniformly convex norms on Banach lattices (Preprint).Google Scholar
3. Gordon, Y. and Lewis, D. R., Absolutely summing operators and local unconditional structures, Acta Math. 133 (1974), 27–48.Google Scholar
4. Gordon, Y. and Lewis, D. R., Banach ideals on Hilbert spaces, Studia Math. 54 (1975), 161–172.Google Scholar
5. Gordon, Y., Lewis, D. R. and Retherford, J. R., Banach ideals of operators with applications, J. of Func. Analysis 14 (1973), 85–129.Google Scholar
6. König, H., Retherford, R. and Tomczak-Jaegerman, N., On the eigenvalues of (p, 2)-summing operators and constants associated to normed spaces. (In preparation.)CrossRefGoogle Scholar
7. Krivine, J. L., Théorèmes de factorization dans les espaces reticules, Séminaire Maurey-Schwartz (1973-74) Exp. 12–13.Google Scholar
8. Krivine, J. L., Sous-espaces de dimension finie des espaces de Banach réticulés, Ann. of Math. 104 (1976), 1–29.Google Scholar
9. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II, function spaces (Springer-Verlag, 1979).CrossRefGoogle Scholar
10. Lozanovskii, G. Y., On some Banach lattices, Siberian Math. J. 10 (1969), 419–430.Google Scholar
11. Lozanovskii, G. Y., On some Banach lattices III, Siberian Math. J. 13 (1971), 910–916.Google Scholar
12. Maurey, B., Type et cotype dans les espaces munis de structures local inconditionelles, Séminaire Maurey-Schwartz (1973-74) exp. 14–15.Google Scholar
13. Maurey, B., Théorèmes de factorization pour les operateurs linéaires a valeurs dans les espaces Lp, Astérisque 11 (1974).Google Scholar
14. Maurey, B. et Pisier, G., Series des variables aléatoires vectorielles independantes et proprietes geometriques des espaces de Banach, Studia Math. 58 (1976), 45–90.Google Scholar
15. Pisier, G., Some application of the complex interpolation method to Banach lattices, Preprint, Centre de Math. Ecole Polytechnique (1979).CrossRefGoogle Scholar
16. Pisier, G., Seminaire d'analyse fone. (1978-79), Exposé 10.Google Scholar
17. Schwartz, L., Seminaire Maurey-Schwartz (1974-75), Exposé 4–6.Google Scholar
18. Vulikh, B. Z., Introduction to the theory of partially ordered spaces. Google Scholar