Article contents
On a Theorem Of Le Roux
Published online by Cambridge University Press: 20 November 2018
Extract
1. The Theorem of Le Roux. Let U(x, y, α) be any solution of the linear hyperbolic differential equation
1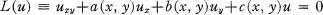
containing a parameter α. J. Le Roux (5) has shown that the function u(x, y) defined by
2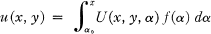 α0 = const.
α0 = const.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1956
References
- 1
- Cited by




