Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T17:06:42.764Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Class of Projectively Flat Metrics with Constant Flag Curvature

Published online by Cambridge University Press:  20 November 2018

Z. Shen  and
G. Civi Yildirim
Z. Shen
Affiliation:
Department of Mathematical Sciences, Indiana University Purdue University Indianapolis (IUPUI), Indianapolis, IN 46202-3216, U.S.A. e-mail: zshen@math.iupui.edu
G. Civi Yildirim
Affiliation:
Department of Mathematics, Faculty of Science and Letters, Istanbul Technical University, Maslak, Istanbul, Turkey e-mail: civi@itu.edu.tr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

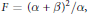In this paper, we find equations that characterize locally projectively flat Finsler metrics in the form $F\,=\,{{(\alpha \,+\,\beta )}^{2}}/\alpha $ where 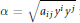$\alpha \,=\,\sqrt{{{a}_{ij}}{{y}^{i}}{{y}^{j}}}$ is a Riemannian metric and 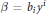$\beta \,=\,{{b}_{i}}{{y}^{i}}$ is a 1-form. Then we completely determine the local structure of those with constant flag curvature.

Keywords

53B40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 2 , 01 April 2008 , pp. 443 - 456
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Berwald, L., Über die n-dimensionalen Geometrien konstanter Krümmung, in denen die Geraden die kürzesten sind. Math. Z. 30(1929), no. 1, 449–469.Google Scholar
[2] Bryant, R., Finsler structures on the 2-sphere satisfying K = 1. In: Finsler Geometry, Contemp. Math. 196, American Mathematical Society, Providence, RI, 1996, pp. 27–42.Google Scholar
[3] Bryant, R., Projectively flat Finsler 2-spheres of constant curvature. Selecta Math. 3(1997), no. 2, 161–203.Google Scholar
[4] Bryant, R., Some remarks on Finsler manifolds with constant flag curvature. Houston J. Math. 28(2002), no. 2, 221–262.Google Scholar
[5] Chen, X., Mo, X., and Shen, Z., On the flag curvature of Finsler metrics of scalar curvature. J. London Math. Soc. 68(2003), no. 3, 762–780.Google Scholar
[6] Chen, X. and Shen, Z., Projectively flat Finsler metrics with almost isotropic S-curvature. Acta Math. Sci. 26(2006), 307–313.Google Scholar
[7] Chern, S. S. and Shen, Z., Riemann-Finsler geometry. Nankai Tracts in Mathematics 6, World Scientific, Hackensack, NJ, 2005.Google Scholar
[8] Hamel, G., Über die Geometrieen, in denen die Geraden die Kürzesten sind. Math. Ann. 57(1903), no. 2, 231–264.Google Scholar
[9] Kitayama, M., Azuma, M., and Matsumoto, M., On Finsler spaces with (α, β)-metric. Regularity, geodesics and main scalars. J. Hokkaido Univ. Ed. Sect. II A 46(1995), no. 1, 1–10.Google Scholar
[10] Matsumoto, M., Finsler spaces with (α, β)-metric of Douglas type. Tensor 60(1998), no. 2, 123–134.Google Scholar
[11] Mo, X., Shen, Z., and Yang, C., Some constructions of projectively flat Finsler metrics. Sci. China Ser. A 49(2006), no. 5, 703–714.Google Scholar
[12] Shen, Z., Projectively flat Randers metrics of constant curvature. Math. Ann. 325(2003), no. 1, 19–30.Google Scholar
[13] Shen, Z., Projectively flat Finsler metrics of constant flag curvature. Trans. Amer.Math. Soc. 355(2003), no. 4, 1713–1728 (electronic).Google Scholar
[14] Shen, Z., Landsberg curvature, S-curvature and Riemann curvature. In: A Sampler of Riemann-Finsler Geometry, Math. Sci. Res. Inst. Publ. 50, Cambridge University Press, Cambridge, 2004.Google Scholar