Hostname: page-component-84b7d79bbc-7nlkj Total loading time: 0 Render date: 2024-07-29T14:34:42.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotency of Some Lie Algebras Associated with p-Groups

Published online by Cambridge University Press:  20 November 2018

Pavel Shumyatsky
Pavel Shumyatsky*
Affiliation:
Department of Mathematics, University of Brasilia, 70.919 Brasilia - DF, Brazil email: pavel@mat.unb.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $L={{L}_{0}}+{{L}_{1}}$ be a 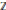${{\mathbb{Z}}_{2}}$ -graded Lie algebra over a commutative ring with unity in which 2 is invertible. Suppose that ${{L}_{0}}$ is abelian and $L$ is generated by finitely many homogeneous elements 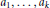${{a}_{1}},.\,.\,.,{{a}_{k}}$ such that every commutator in 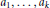${{a}_{1}},.\,.\,.,{{a}_{k}}$ is ad-nilpotent. We prove that $L$ is nilpotent. This implies that any periodic residually finite 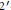${2}'$ -group $G$ admitting an involutory automorphism $\phi $ with 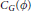${{C}_{G}}\left( \phi \right)$ abelian is locally finite.

Keywords

17B7020F50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 658 - 672
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Aleshin, S. V., Finite automata and the Burnside problem for periodic groups. Math. Notes 11 (1972), 199–203.Google Scholar
[2] Deryabina, G. S. and Ol’shanskii, A. Yu., Subgroups of quasifinite group. (in Russian). Uspekhi Math. Nauk. 41 (1986), 169–170.Google Scholar
[3] Golod, E. S., On nil-algebras and residually finite groups. Izv. Akad. Nauk SSSR, Ser.Mat.. 28 (1964), 273–276.Google Scholar
[4] Grigorchuk, R. I., On the Burnside problem for periodic groups. Funct. Anal. Appl.. 14 (1980), 53–54.Google Scholar
[5] Gupta, N. and Sidki, S., On the Burnside problem for periodic groups. Math. Z.. 182 (1983), 385–386.Google Scholar
[6] Huppert, B. andBlackburn, N., Finite groups II Springer, Berlin, 1982.Google Scholar
[7] Kostrikin, A. I., Around Burnside (transl. Wiegold, J.). Springer, Berlin, 1990.Google Scholar
[8] Kov´acs, L. G. and Wall, G. E., Involutory automorphisms of groups of odd order and their fixed point groups. Nagoya Math. J.. 27 (1966), 113–120.Google Scholar
[9] Lazard, M., Sur les groupes nilpotents et les anneaux de Lie. Ann. Sci. École Norm. Sup.. 71 (1954), 101–190.Google Scholar
[10] Neumann, B. H., On the commutativity of addition. J. LondonMath. Soc.. 15 (1940), 203–208.Google Scholar
[11] Rocco, N. R. and Shumyatsky, P., On periodic groups having almost regular 2-elements. Proc. EdinburghMath. Soc.. 41 (1998), 385–391.Google Scholar
[12] Shumyatsky, P. V., Periodic groups with a regular four-group of automorphisms. Soviet Math (Iz. VUZ) (11). 31 (1987), 102–107.Google Scholar
[13] Shumyatsky, P. V., Local finiteness of some groups with a regular four-group of automorphisms (in Russian). In: Algebraic systems and their varieties, Sverdlovsk, 1988, 171–180.Google Scholar
[14] Shumyatsky, P. V., Groups and Lie algebras with a fixed-point-free four-group of automorphisms. Comm. Algebra (12). 24 (1996), 3771–3785.Google Scholar
[15] Shumyatsky, P. V., On groups having a four-subgroup with finite centralizer. Quart. J. Math, to appear.Google Scholar
[16] Šunkov, V. P., On periodic groups with an almost regular involution. Algebra and Logic. 11 (1972), 260–272.Google Scholar
[17] Sushchansky, V. I., Periodic p-elements of permutations and the general Burnside problem. Dokl. Akad. Nauk SSSR. 247 (1979), 447–461.Google Scholar
[18] Zelmanov, E., Lie ring methods in the theory of nilpotent groups. In: Groups ‘93, Galway-St Andrews, London Math. Soc. Lecture Note Ser.. 212 (1995), 567–586.Google Scholar