Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Su, Yucai
Xu, Xiaoping
and
Zhang, Hechun
2000.
Derivation-Simple Algebras and the Structures of Lie Algebras of Witt Type.
Journal of Algebra,
Vol. 233,
Issue. 2,
p.
642.
Zhao, Kaiming
2001.
Simple algebras of Weyl type, II.
Proceedings of the American Mathematical Society,
Vol. 130,
Issue. 5,
p.
1323.
Su, Yucai
and
Zhao, Kaiming
2001.
Simple algebras of Weyl type.
Science in China Series A: Mathematics,
Vol. 44,
Issue. 4,
p.
419.
Su, Yucai
and
Zhou, Jianhua
2001.
Some Representations of Nongraded Lie Algebras of Generalized Witt Type.
Journal of Algebra,
Vol. 246,
Issue. 2,
p.
721.
Su, Yucai
and
Zhao, Kaiming
2002.
Isomorphism classes and automorphism groups of algebras of Weyl type.
Science in China Series A: Mathematics,
Vol. 45,
Issue. 8,
p.
953.
Su, Yucai
and
Zhao, Kaiming
2002.
SECOND COHOMOLOGY GROUP OF GENERALIZED WITT TYPE LIE ALGEBRAS AND CERTAIN REPRESENTATIONS.
Communications in Algebra,
Vol. 30,
Issue. 7,
p.
3285.
Su, Yucai
2003.
Derivations of generalized Weyl algebras.
Science China Mathematics,
Vol. 46,
Issue. 3,
p.
346.
BAVULA, V. V.
2017.
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS.
Glasgow Mathematical Journal,
Vol. 59,
Issue. 3,
p.
513.
Bavula, V. V.
2017.
The group of automorphisms of the Lie algebra of derivations of a polynomial algebra.
Journal of Algebra and Its Applications,
Vol. 16,
Issue. 05,
p.
1750088.
Liu, Genqiang
Lu, Rencai
and
Zhao, Kaiming
2018.
Irreducible Witt modules from Weyl modules andgln-modules.
Journal of Algebra,
Vol. 511,
Issue. ,
p.
164.
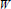 $W$ Lie algebras
$W$ Lie algebras 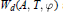 ${{W}_{d}}(A,\,T,\,\varphi )$ are isomorphic, and discuss the relationship between the Jacobian conjecture and the generalized Cartan type
${{W}_{d}}(A,\,T,\,\varphi )$ are isomorphic, and discuss the relationship between the Jacobian conjecture and the generalized Cartan type 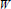 $W$ Lie algebras.
$W$ Lie algebras.



