Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T13:31:46.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Fubini's Theorem for Ultraproducts of Noncommutative Lp-Spaces

Published online by Cambridge University Press:  20 November 2018

Marius Junge
Marius Junge*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, U.S.A. e-mail: junge@math.uiuc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

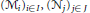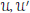Let ${{({{\mathcal{M}}_{i}})}_{i}}{{_{\in }}_{I}},{{({{\mathcal{N}}_{j}})}_{j\in J}}$ be families of von Neumann algebras and $\mathcal{U},\,{\mathcal{U}}'$ be ultrafilters in 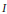$I$, 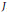$J$, respectively. Let 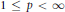$1\,\le \,p\,<\,\infty $ and 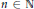$n\,\in \,\mathbb{N}$. Let 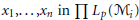${{x}_{1}},...,{{x}_{n}}\,\text{in}\,\prod {{L}_{p}}({{\mathcal{M}}_{i}})$ and 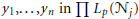${{y}_{1}},...,{{y}_{n\,}}\text{in }\Pi \,{{L}_{p}}({{\mathcal{N}}_{j}})$ be bounded families. We show the following equality

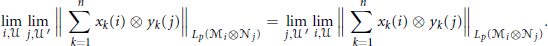$$\underset{i,\mathcal{U}}{\mathop{\lim }}\,\,\underset{j,{\mathcal{U}}'}{\mathop{\lim }}\,\,{{\left\| \sum\limits_{k=1}^{n}{{{x}_{k}}(i)\,\otimes \,{{y}_{k}}(j)} \right\|}_{{{L}_{p}}({{\mathcal{M}}_{i}}\otimes {{\mathcal{N}}_{j}})}}=\,\underset{j,{\mathcal{U}}'}{\mathop{\lim }}\,\,\underset{i,\mathcal{U}}{\mathop{\lim }}\,\,{{\left\| \sum\limits_{k=1}^{n}{{{x}_{k}}(i)\,\,\otimes \,{{y}_{k}}(j)} \right\|}_{{{L}_{p}}({{\mathcal{M}}_{i}}\otimes {{\mathcal{N}}_{j}})}}$$

For 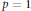$p\,=\,1$ this Fubini type result is related to the local reflexivity of duals of 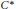${{C}^{*}}$ -algebras. This fails for 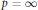$P=\infty $.

Keywords

46L5246B0846L07noncommutativeLp-spacesultraproducts
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 5 , 01 October 2004 , pp. 983 - 1021
Copyright
Copyright © Canadian Mathematical Society 2004

References

[BL] Bergh, J. and Löfström, J., Interpolation spaces. An introduction; Grundlehren der Mathematischen Wissenschaften 223, Springer-Verlag, Berlin, 1976.Google Scholar
[BP] Blecher, D. P. and Paulsen, V. I., Tensor products of operator spaces. J. Funct. Anal. 99(1991), 262–292.Google Scholar
[Ch] Choi, M. D., A Schwarz inequality for positive linear maps on C*-algebras, Illinois J. Math 18, 565–574.Google Scholar
[C1] Connes, A., Classification of injective factors. Cases II 1, II ∞, III λ , λ ≠ 1 . Ann. of Math. 104(1976), 73–115.Google Scholar
[C2] Connes, A., Sur la théorie non commutative de l’integration; Algèbres d’opérateurs, Semin. Les Plans-sur-Bex 1978, Lect. Notes Math. 725, 19–143 (1979).Google Scholar
[C3] Connes, A., Noncommutative Geometry Academic Press, 1994.Google Scholar
[Dx] Dixmier, J., Von Neumann Algebras. North Holland, Amsterdam, 1981.Google Scholar
[EJR] Effros, E., Junge, M. and Ruan, Z. J., Integral mappings and the principle of local refelxivity for noncommutative L 1 -spaces. Annals of Math. 151(2000), 59–92.Google Scholar
[ER2] Effros, E. and Ruan, Z-J., On approximation properties of operator spaces. Internat. J. Math. 1(1990), 163–187.Google Scholar
[ER3] Effros, E. and Ruan, Z-J., Operator spaces, London Math. Soc. Monographs New Series 23, Oxford University Press, 2000.Google Scholar
[Fi] Fidaleo, F., Canonical operator space structures on non-commutative Lp spaces. J. Funct. Anal. 169(1999), 226–250.Google Scholar
[Gr] Groh, U., Uniform ergodic theorems for identity preserving Schwartz maps on W*-algebras. J. Operator Theory 11(1984), 396–404.Google Scholar
[Ha1] Haagerup, U., A new proof of the equivalence of injectivity and hyperfiniteness for factors on a separable Hilbert space. J. Funct. Anal. 62(1985), 160–201.Google Scholar
[Ha2] Haagerup, U., Lp-spaces associated with an arbitrary von Neumann algebra. Algébres d’opérateurs et leurs applications en physique mathématique (Proc. Colloq., Marseille, 1977), pp. 175–184, Colloq. Internat. CNRS, 274, CNRS, Paris, 1979.Google Scholar
[J1] Junge, M., Doob's inequality for non-commutative martingales. J. Reine Angew. Math 549(2002), 149–190.Google Scholar
[J2] Junge, M., Applications of the Fubini theorem for non-commutative Lp spaces; preprint.Google Scholar
[JNRX] Junge, M., Nielsen, N. J., Ruan, Z. J. and Xu, Q., The local structure of non-commutative Lp spaces. to appear in Advances of Mathematics.Google Scholar
[JR] Junge, M. and Ruan, Z. J., Approximation properties for non-commutative Lp spaces associated to discrete groups. Duke Math. J. 117(2003), 313–341.Google Scholar
[JX] Junge, M. and Xu, Q.. Non-commutative Burkholder/Rosenthal inequalities. Annals of Probability 31(2003), 948–995.Google Scholar
[Ki] Kirchberg, E., On nonsemisplit extensions, tensor products and exactness of group C*-algebras. Invent. Math. 112(1993), no. 3,Google Scholar
[Ko] Kosaki, H., Applications of the Complex Interpolation Method to a von Neumann Algebra: Non-commutative Lp-spaces. J. Funct. Anal. 56(1984), 29–78.Google Scholar
[Ko2] Kosaki, H., On the continuity of the map φ → |φ| from the predual of aW*-algebra. J. Funct. Anal. 59(1984), 123–131.Google Scholar
[KR] Kadison, R. and Ringrose, J., Fundamentals of the theory of operator algebras I and II. Graduate Studies in Mathematics 15 and 16, AMS, Providence, RI, 1997 Google Scholar
[Ne] Nelson, E., Notes on non-commutative integration. J. Funct. Anal. 15(1974), 103–116.Google Scholar
[Pa] Paulsen, V. I., Completely bounded maps and dilations. Pitman Research Notes in Mathematics, 1986.Google Scholar
[PT ] Pedersen, G. and Takesaki, M., The Radon-Nikodym theorem for von Neumann algebras. Acta Math. 130(1973), 53–87.Google Scholar
[P6] Pisier, G., The operator Hilbert space OH, complex interpolation and tensor norms. Memoirs Amer. Math. Soc. 585, Vol 122, July 1996.Google Scholar
[P7] Pisier, G., Noncommutative vector valued integration and completely p-summing maps. Astérisque No. 247, (1998).Google Scholar
[P8] Pisier, G., Introduction to operator spaces; preprint.Google Scholar
[R1] Ruan, Z. J., Subspaces of C*-algebras. J. Funct. Anal. (1988), 217–230.Google Scholar
[Ra2] Raynaud, Y., On ultrapowers of non-commutative Lp-spaces. J. Operator Theory 48(2002), 41–68.Google Scholar
[Se] Segal, I. E., A non-commutative extension of abstract integration. Ann. Math. 57(1953), 401–457.Google Scholar
[Te1] Terp, M., Lp-spaces associated with von Neumann algebras I and II; Copenhagen Univ. 1981.Google Scholar
[Tk] Takesaki, M., Theory of operator algebras I. Springer-Verlag, New York, 1979.Google Scholar
[Wa] Wassermann, S.. On tensor products of certain group C*-algebras. J. Funct. Analysis 23(1976), 239–254.Google Scholar