Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-02T04:30:28.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Positive Global Solutions of Mixed Sublinear-Superlinear Problems

Published online by Cambridge University Press:  20 November 2018

W. Allegretto  and
Y. X. Huang
W. Allegretto
Affiliation:
University of Alberta, Edmonton, Alberta
Y. X. Huang
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the elliptic quasilinear problem:

1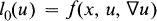

in Rn, n ≧ 3, where

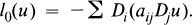
We are interested in establishing sufficient conditions on f for the existence of positive solutions u(x) with specified behaviour at ∞. Of special interest to us are criteria which guarantee that u(x) decays at least as fast as |x|−α for some α ≧ 0, given below, in the case f(x, u, ∇u) contains terms of type

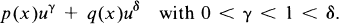
That is: f is of mixed sublinear-super linear type. Our main result is Theorem 3 below which explicitly states sufficient conditions for the existence of such solutions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1222 - 1242
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Allegretto, W., On positive L∞ solutions of a class of elliptic systems, Math. Z. 191 (1986), 479–484.Google Scholar
2. Allegretto, W., Criticality and the λ-property for elliptic equations, J. Differential Equations 69 (1987), 39–45.Google Scholar
3. Boccardo, L., Murat, F. and Puel, J. P., Resultants d'existence pour certains problèmes elliptiques quasilinèaires, Ann. Scuola Norm. Sup. Pisa CI. Ser. IV, XI (1984), 213–235.Google Scholar
4. Brezis, H. and Turner, R. E. L., On a class of superlinear elliptic problems, Comm. in P.D.E. 2 (1977), 601–614.Google Scholar
5. de Figueiredo, D. G., Lions, P.-L. and Nussbaum, R. D., A priori estimates and existence of positive solutions of semilinear equations, J. Math. Pures et Appl. 61 (1982), 41–63.Google Scholar
6. Ding, W.-Y. and Ni, W. M., On the elliptic equation Δu + ku(n + 2)/(n − 2) = 0 and related topics, Duke Math. J. 52 (1985), 485–506.Google Scholar
7. Donato, P. and Giachetti, P., Quasilinear elliptic equations with quadratic growth in unbounded domains, Nonlinear Anal. 10 (1986), 791–804.Google Scholar
8. Fukagai, N., Existence and uniqueness of entire solutions of second order sublinear elliptic equations, Funkcial. Ekvac. 29(1986), 151–165.Google Scholar
9. Fukagai, N., Kusano, T. and Yoshida, K., Some remarks on the supersolution-subsolution method for sup erlinear elliptic equations, J. Math. Anal. Appl. 123 (1987), 131–141.Google Scholar
10. Furusho, Y., Existence of global positive solutions of quasilinear elliptic equations in unbounded domains, Japan J. Math. 14 (1988), 97–118.Google Scholar
11. Gidas, B. and Spruck, J., Global and local behaviour of positive solutions of nonlinear elliptic equations, Comm. Pure Appl. Math. 34 (1981), 525–598.Google Scholar
12. Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order, second edition (Springer-Verlag, N.Y., 1983).CrossRefGoogle Scholar
13. Hess, P., On a second-order nonlinear elliptic boundary value problem, in Nonlinear analysis (Academic Press, N.Y., 1978), 99–107.Google Scholar
14. Hess, P., Nonlinear elliptic problems in unbounded domains, in Theory of nonlinear operators (Abh. Wiss. DDR. 1977, 1, Akademie-Verlag, Berlin, 1977), 105–110.Google Scholar
15. Joseph, D. D. and Lundgren, T. S., Quasilinear Dirichlet problems driven by positive sources, Arch. Rational Mech. Anal. 49 (1973), 241–269.Google Scholar
16. Kawano, N., On bounded entire solutions of semilinear elliptic equations, Hiroshima Math. J. 74(1984), 125–158.Google Scholar
17. Kawano, N., T. Kusano and M. Naito, On the elliptic equation Δu = φ(x)uγ in R 2 , Proc. Amer. Math. Soc. 93 (1985), 73–78.Google Scholar
18. Kusano, T. and Oharu, S., Bounded entire solutions of second order semilinear elliptic equations with application to a parabolic initial value problem, Indiana Univ. Math. J. 34(1985), 85–95.Google Scholar
19. Kusano, T. and Oharu, S., On entire solutions of second order semilinear elliptic equations, J. Math. Anal. Appl. 113 (1986), 123–135.Google Scholar
20. Kusano, T. and Swanson, C. A., Entire positive solutions of singular semilinear elliptic equations, Japan J. Math. 11 (1985), 145–155.Google Scholar
21. Kusano, T. and Swanson, C. A., Decaying entire positive solutions of quasilinear elliptic equations, Monatsh. Math. 101 (1986), 39–51.Google Scholar
22. Kusano, T. and Trench, W. F., Global existence of solutions of mixed sublinear-sup erlinear differential equations, Hiroshima Math. J. 16 (1986), 597–606.Google Scholar
23. Ladyzhenskaya, O. and Ural'tseva, N., Linear and quasilinear elliptic equations (Academic Press, N.Y., 1968).Google Scholar
24. Ni, W. M., On the elliptic equation Δu + k(x)u(n + 2)/(n − 2) = 0, its generalizations and application in geometry, Indiana Univ. Math. J. 31 (1982), 493–529.Google Scholar
25. Noussair, E. S. and Swanson, C. A., Global positive solutions of semilinear elliptic equations, Can. J. Math. 35 (1983), 839–861.Google Scholar
26. Noussair, E. S. and Swanson, C. A., Positive Lq(R n)-solutions of subcritical Emden-Fowler problems, Arch. Rat. Mech. Anal. 101 (1988), 85–93.Google Scholar
27. Swanson, C. A., Positive solutions of —Δu = f(x, u), Nonlinear Anal. 9 (1985), 1319–1323.Google Scholar
28. Usami, H., On bounded positive entire solutions of semilinear elliptic equations, Funkcial. Ekvac. 29 (1986), 189–195.Google Scholar