Article contents
Eigenvarieties for Cuspforms Over PELType Shimura Varieties With Dense Ordinary Locus
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 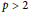 $p\,>\,2$ be a prime and let
$p\,>\,2$ be a prime and let  $X$ be a compactified PEL Shimura variety of type
$X$ be a compactified PEL Shimura variety of type 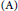 $\left( \text{A} \right)$ or
$\left( \text{A} \right)$ or 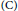 $\left( \text{C} \right)$ such that
$\left( \text{C} \right)$ such that 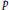 $p$ is an unramified prime for the PEL datum and such that the ordinary locus is dense in the reduction of
$p$ is an unramified prime for the PEL datum and such that the ordinary locus is dense in the reduction of  $X$. Using the geometric approach of Andreatta, Iovita, Pilloni, and Stevens, we define the notion of families of overconvergent locally analytic
$X$. Using the geometric approach of Andreatta, Iovita, Pilloni, and Stevens, we define the notion of families of overconvergent locally analytic 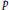 $p$-adic modular forms of Iwahoric level for
$p$-adic modular forms of Iwahoric level for  $X$. We show that the system of eigenvalues of any finite slope cuspidal eigenform of Iwahoric level can be deformed to a family of systems of eigenvalues living over an open subset of the weight space. To prove these results, we actually construct eigenvarieties of the expected dimension that parameterize finite slope systems of eigenvalues appearing in the space of families of cuspidal forms.
$X$. We show that the system of eigenvalues of any finite slope cuspidal eigenform of Iwahoric level can be deformed to a family of systems of eigenvalues living over an open subset of the weight space. To prove these results, we actually construct eigenvarieties of the expected dimension that parameterize finite slope systems of eigenvalues appearing in the space of families of cuspidal forms.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 3
- Cited by


