Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T13:45:12.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion on Lie Groups II

Published online by Cambridge University Press:  20 November 2018

N. TH. Varopoulos
N. TH. Varopoulos*
Affiliation:
Université de Paris VI, 4 Place Jussieu 75005 Paris, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The heat kernel of an amenable Lie group satisfies either exp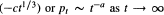. We give a condition on the Lie algebra which characterizes the two cases.

Résumé

Résumé

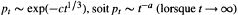Pour le noyau de la chaleur sur un groupe de Lie moyennable on a soit . On donne une condition sur l'algèbre de Lie qui caracterise les deux cas.

Keywords

22E3043A8060J6060J65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 5 , 01 October 1994 , pp. 1073 - 1092
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Varopoulos, N. Th., Analysis on Lie groups, J. Funct. Anal. (2) 76(1988), 346–410.Google Scholar
2. Varopoulos, N. Th., Saloff-Coste, L. and Coulhon, T., Analysis and geometry on groups, Cambridge Univ. Press, 1992.Google Scholar
3. Hörmander, L., Hypoelliptic second order operators, Acta Math. 119(1967), 147–171.Google Scholar
4. Varadarajan, V. S., Lie groups, Lie algebras and their representations, Prentice-Hall, 1984.Google Scholar
5. Jacobson, N., Lie algebras, Interscience, 1962.Google Scholar
6. Chevalley, C., Théorie de groupes de Lie, tome HI, Hermann, 1955.Google Scholar
7. Reiter, H., Classical harmonie analysis and locally compact groups, Oxford, Math. Monograph, 1968.Google Scholar
8. Varopoulos, N. Th., Diffusion on Lie groups, Canad. J. Math. (2) 46(1994), 438–448.Google Scholar
9. Alexopoulos, G., Fonctions harmoniques bornées sur les groupes résolubles, C. R. Acad. Sci. Paris 305 (1987), 777–779.Google Scholar
10. Alexopoulos, G., A lower estimate for central probability on polycyclic group, Canad. J. Math. (5) 44(1992), 897–910.Google Scholar
11. Hebisch, W., On heat kernels on Lie groups, preprint.Google Scholar
12. Guivarc'h, Y., Croissance polynômiale et périodes des fonctions harmoniques, Bull. Soc. Math. France 101(1973), 333–379.Google Scholar
13. Alexopoulos, G., An application of homogenization theory to harmonie analysis: Harnack inequalities and Riesz transforms on Lie groups of polynomial growth, Canad. J. Math. (4) 44(1992), 691–727.Google Scholar
14. Ibragimov, I. A. and Linnik, Yu. V., Independent and stationary sequences of random variables, Wolters-Noordhoff, 1971.Google Scholar
15. Varopoulos, N. Th., A potential theoretic property of soluble groups, Bull. Sci. Math. (2) 108(1983), 263–273.Google Scholar
16. Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces, Princeton Univ. Press, 1971.Google Scholar
17. Szegö, G., Orthogonal polynomials, Amer. Math. Soc. Colloq. Publ. XXIII, 1939.Google Scholar
18. Hörmander, L., Estimates for translation invariant operators in LP spaces, Acta Math. 104(1960), 93–139.Google Scholar
19. Varopoulos, N. Th., Sobolev inequalities on Lie groups and symmetric spaces, J. Funct. Anal. 86(1989), 19–40.Google Scholar
20. Varopoulos, N. Th., Théorie de Hardy-Littlewood sur les groupes de Lie, C. R. Acad. Sci. Paris Ser. I 316(1993), 999–1003.Google Scholar