Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T11:14:09.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteria for Groups with Representations of the Second Kind and for Simple Phase Groups

Published online by Cambridge University Press:  20 November 2018

A. J. Van Zanten  and
E. De Vries
A. J. Van Zanten
Affiliation:
Department of Physics, Duke University, Durham, North Carolina
E. De Vries
Affiliation:
Department of Physics, Duke University, Durham, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider matrix representations of compact groups over the field of the complex numbers. We shall deal mainly with finite groups.

The Kronecker product of two irreducible representations σ1 and σ2 of a group 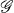is in general a reducible representation of 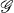. The explicit reduction of such a product to irreducible representations σ3 can be performed by means of a unitary matrix, the elements of which are called Wigner coefficients or Clebsch-Gordan coefficients [1; 25; 27].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 3 , 01 June 1975 , pp. 528 - 544
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Biedenharn, L. C. and van Dam, H. (eds.), Quantum theory of angular momentum (Academic Press, New York-London, 1965).Google Scholar
2. Biedenharn, L. C., Nuyts, J., and Ruegg, H., On generalizations of isoparity, Comm. Math. Phys. 2 (1966), 231–250.Google Scholar
3. Bose, A. K. and Patera, J., Classification of finite-dimensional irreducible representations of connected complex semisimple Lie groups, J. Mathematical Phys. 7 (1970), 2231–2234.Google Scholar
4. Burnside, W., Theory of groups of finite order, 2nd edition (Dover Publ., New York, 1955),Google Scholar
5. Burrow, M., Representation theory of finite groups (Academic Press, New York-London, 1965).Google Scholar
6. Butler, P. H., Wigner coefficients and n — j symbols for chains of groups (to appear).Google Scholar
7. Butler, P. H. and King, R. C., Symmetrized Kronecker products of group representations, J. Mathematical Phys. U (1973), 1176–1183.Google Scholar
8. Coxeter, H. L.M. and Moser, W. O. J., Generators and relations for discrete groups, 2nd edition (Springer Verlag, Berlin-Gottingen-Heidelberg-New York, 1965).Google Scholar
9. Derome, J.-R. and Sharp, W. T., Racah algebra for an arbitrary group, J. Mathematical Phys. 6 (1965), 1584–1590.Google Scholar
10. Derome, J.-R., Symmetry properties of the Sj-symbols for an arbitrary group, J. Mathematical Phys. 7 (1966), 612–615.Google Scholar
11. Feit, W., Characters of finite groups (W. A. Benjamin, New York-Amsterdam, 1967).Google Scholar
12. Frobenius, G. and Schur, I., Uber die reellen Darstellungen der endlichen Gruppen, Sitzungsberichte der kôn. preuss. Ak. der Wissenschaften (1906), 186–208.Google Scholar
13. Hall, M. Jr., The theory of groups (Macmillan Co., New York, 1964).Google Scholar
14. Hall, M. Jr., and Wales, D., The simple group of order 604,800, J. Algebra 9 (1968), 417–450.Google Scholar
15. Huppert, B., Endliche Gruppen, I (Springer Verlag, Berlin-Heidelberg-New York, 1955).Google Scholar
16. King, R. C., Branching rules far (GL(N) 2) £ m and the evaluation of inner plethysms, J. Mathematical Phys. 15 (1974), 258–267.Google Scholar
17. Ledermann, W., Introduction to the theory of finite groups, 5th edition (Oliver and Boyd, Edinburgh-London, 1964).Google Scholar
18. Mackey, G. W., Symmetric and antisymmetric Kronecker squares and intertwining numbers of induced representations of finite groups, Amer. J. Math. 75 (1953), 387–405.Google Scholar
19. Mal'cev, A. I., On semi-simple subgroups of Lie groups, Izv. Akad. Nauk. SSSR ser. Mat. 8 (1944), 143–174 [Am. Math. Soc. Transi, no. 23 (1950)].Google Scholar
20. Mehta, M. L., Classification of irreducible unitary representations of compact simple Lie groups. I, J. Mathematical Phys. 7 (1966), 1824–1832.Google Scholar
21. Mehta, M. L. and Srivastava, P. K., Classification of irreducible representations of compact simple Lie groups. II, J. Mathematical Phys. 7 (1966), 1833–1835.Google Scholar
22. Schur, I., Arithmetische Untersuchungen uber endliche Gruppen linearer Substitutionen, Sitzungsberichte der kon. preuss. Ak. der Wissenschaften (1906), 164–184 (Berlin).Google Scholar
23. van Zanten, A. J., Some applications of the representation theory of finite groups: a partial reduction method, Ph.D. thesis, Groningen, 1972.Google Scholar
24. van, A. J. Zanten and de Vries, E., On the number of roots of the equation Xn= 1 infinite groups and related properties, J. Algebra 25 (1973), 475–486.Google Scholar
25. van, A. J. Zanten and de Vries, E., On the number of classes of a finite group invariant for certain substitutions, Can. J. Math. 26 (1974), 1090–1097.Google Scholar
26. Wigner, E. P., On the matrices which reduce the Kronecker products of representations of S.R. groups (Princeton, 1951, reprinted in ref. 1).Google Scholar
27. Wigner, E. P., Group theory and its application to the quantum mechanics of atomic spectra (Academic Press, New York-London, 1959).Google Scholar
28. Wigner, E. P., On representations of certain finite groups, Amer. J. Math. 63 (1941), 57–63 (reprinted in ref. 1).Google Scholar