Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Elliott, George A.
Gong, Guihua
and
Li, Liangqing
2007.
On the classification of simple inductive limit C*-algebras, II: The isomorphism theorem.
Inventiones mathematicae,
Vol. 168,
Issue. 2,
p.
249.
Toms, Andrew S.
2007.
Dimension growth forC∗-algebras.
Advances in Mathematics,
Vol. 213,
Issue. 2,
p.
820.
Phillips, N.
2007.
Recursive subhomogeneous algebras.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 10,
p.
4595.
Elliott, George A.
and
Ivanescu, Cristian
2008.
The classification of separable simple C∗-algebras which are inductive limits of continuous-trace C∗-algebras with spectrum homeomorphic to the closed interval [0,1].
Journal of Functional Analysis,
Vol. 254,
Issue. 4,
p.
879.
Toms, Andrew S.
and
Winter, Wilhelm
2008.
-Stable ASH Algebras.
Canadian Journal of Mathematics,
Vol. 60,
Issue. 3,
p.
703.
Lin, Huaxin
2010.
Inductive limits of subhomogeneous C∗-algebras with Hausdorff spectrum.
Journal of Functional Analysis,
Vol. 258,
Issue. 6,
p.
1909.
Lin, Huaxin
and
Niu, Zhuang
2011.
The range of a class of classifiable separable simple amenableC∗-algebras.
Journal of Functional Analysis,
Vol. 260,
Issue. 1,
p.
1.
Lin, Huaxin
2011.
Asymptotic unitary equivalence and classification of simple amenable C ∗-algebras.
Inventiones mathematicae,
Vol. 183,
Issue. 2,
p.
385.
Elliott, George A.
and
Li, Zhiqiang
2015.
The KK-lifting problem for dimension drop interval algebras.
Journal of Functional Analysis,
Vol. 268,
Issue. 4,
p.
847.
An, Qingnan
Elliott, George A.
Li, Zhiqiang
and
Liu, Zhichao
2022.
The classification of certain ASH C*-algebras of real rank zero.
Journal of Topology and Analysis,
Vol. 14,
Issue. 01,
p.
183.
An, Qingnan
and
Liu, Zhichao
2023.
On the Range of Certain ASH Algebras of Real Rank Zero.
Chinese Annals of Mathematics, Series B,
Vol. 44,
Issue. 2,
p.
279.
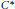 ${{C}^{*}}$-algebras that are simple unital infinite dimensional inductive limits of finite direct sums of building blocks of the form
${{C}^{*}}$-algebras that are simple unital infinite dimensional inductive limits of finite direct sums of building blocks of the form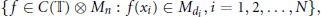 $$\left\{ f\in C\left( \mathbb{T} \right)\otimes {{M}_{n}}:f\left( {{x}_{i}} \right)\in {{M}_{{{d}_{i}}}},i=1,2,...,N \right\},$$
$$\left\{ f\in C\left( \mathbb{T} \right)\otimes {{M}_{n}}:f\left( {{x}_{i}} \right)\in {{M}_{{{d}_{i}}}},i=1,2,...,N \right\},$$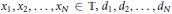 ${{x}_{1}},\,{{x}_{2.}},...,{{x}_{N\,}}\in \mathbb{T},{{d}_{1}},{{d}_{2}},.\,.\,.,{{d}_{N}}$ are integers dividing
${{x}_{1}},\,{{x}_{2.}},...,{{x}_{N\,}}\in \mathbb{T},{{d}_{1}},{{d}_{2}},.\,.\,.,{{d}_{N}}$ are integers dividing 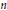 $n$, and
$n$, and 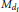 ${{M}_{{{d}_{i}}}}$ is embedded unitally into
${{M}_{{{d}_{i}}}}$ is embedded unitally into 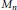 ${{M}_{n}}$. Furthermore we prove existence and uniqueness theorems for
${{M}_{n}}$. Furthermore we prove existence and uniqueness theorems for  $*$-homomorphisms between such algebras and we identify the range of the invariant.
$*$-homomorphisms between such algebras and we identify the range of the invariant.



