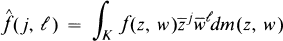Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nakazi, Takahiko
and
Takahashi, Katsutoshi
1991.
Homogeneous polynomials and invariant subspaces in the polydisc. II.
Proceedings of the American Mathematical Society,
Vol. 113,
Issue. 4,
p.
991.
Nakazi, Takahiko
1992.
Homogeneous polynomials and invariant subspaces in the polydisc.
Archiv der Mathematik,
Vol. 58,
Issue. 1,
p.
56.
Nakazi, Takahiko
1994.
Multipliers of invariant subspaces in the bidisc.
Proceedings of the Edinburgh Mathematical Society,
Vol. 37,
Issue. 2,
p.
193.
Nakazi, Takahiko
1994.
Invariant subspaces in the bidisc and commutators.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 56,
Issue. 2,
p.
232.
Izuchi, Keiji
and
Ohno, Sh�ichi
1997.
Selfadjoint commutators and invariant subspaces on the torus II.
Integral Equations and Operator Theory,
Vol. 27,
Issue. 2,
p.
208.
Ji, Guoxing
Ohwada, Tomoyoshi
and
Saito, Kichi-Suke
1998.
Certain invariant subspace structure of 𝐿²(𝕋²).
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 8,
p.
2361.
Nakazi, Takahiko
2004.
Factorizations of functions in Hp (Tn ).
Complex Variables, Theory and Application: An International Journal,
Vol. 49,
Issue. 5,
p.
323.
SETO, Michio
2005.
Submodules of $L^2(\mathbf{R}^2)$.
Tokyo Journal of Mathematics,
Vol. 28,
Issue. 2,
NAKAZI, TAKAHIKO
2008.
INVARIANT SUBSPACES IN THE BIDISC AND WANDERING SUBSPACES.
Journal of the Australian Mathematical Society,
Vol. 84,
Issue. 03,
Nakazi, Takahiko
2011.
Multipliers of a wandering subspace for a shift invariant subspace.
Journal of Mathematical Analysis and Applications,
Vol. 377,
Issue. 1,
p.
251.
Izuchi, Kei Ji
Izuchi, Kou Hei
and
Izuchi, Yuko
2011.
Blaschke products and the rank of backward shift invariant subspaces over the bidisk.
Journal of Functional Analysis,
Vol. 261,
Issue. 6,
p.
1457.
Izuchi, Kei Ji
and
Izuchi, Kou Hei
2012.
Commutativity in two-variable Jordan blocks on the Hardy space.
Acta Scientiarum Mathematicarum,
Vol. 78,
Issue. 1-2,
p.
129.
Izuchi, Kei Ji
Izuchi, Kou Hei
and
Izuchi, Yuko
2016.
Invariant subspaces having two side frames over the bidisk.
Journal of Mathematical Analysis and Applications,
Vol. 436,
Issue. 2,
p.
1102.
Anand, Jatin
Sahni, Niteesh
and
Srivastava, Sachi
2021.
On extension of Beurling–Helson–Lowdenslager theorem.
Advances in Operator Theory,
Vol. 6,
Issue. 4,
Dan, Hui
and
Guo, Kunyu
2023.
Dilation theory and analytic model theory for doubly commuting sequences of C·0-contractions.
Science China Mathematics,
Vol. 66,
Issue. 2,
p.
303.