Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-13T19:02:09.067Z Has data issue: false hasContentIssue false
  • English
  • Français

The Approximate Symmetric Integral

Published online by Cambridge University Press:  20 November 2018

D. Preiss  and
B. S. Thomson
D. Preiss
Affiliation:
Charles University, Praha 8, Czechoslovakia
B. S. Thomson
Affiliation:
Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a symmetric integral is understood an integral obtained from some kind of symmetric derivation process. Such integrals arise most naturally in the study of trigonometric series and in particular to handle the following problem. Suppose that a trigonometric series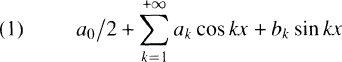

converges everywhere to a function À. It is known that this may occur without À being integrable in any of the more familiar senses so that the series may not be considered as a Fourier series of À; indeed Denjoy [4] has shown that if bnis a sequence of real numbers decreasing to zero but with

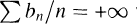+00 then the function À(x) = 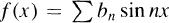is not Denjoy-integrable. It is natural to ask then for an integration procedure that can be applied to À in order that the series be the Fourier series of À with respect to this integral.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 3 , 01 June 1989 , pp. 508 - 555
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Burkill, J.C., The Cesàro-Perron integral, Proc. London Math. Soc. (2) 34 (1932), 314–322.Google Scholar
2. Burkill, J.C., Integrals and trigonometric series, Proc. London Math. Soc. (3) 7 (1951), 46–57.Google Scholar
3. Cross, G.E., On the generality of the AP-integral, Canadian J. Math. 23 (1971), 557–561.Google Scholar
4. Denjoy, A., Leçons sur le calcul des coefficients d'une série trigonométrique Ensembles Parfait et séries trigonométriques (Hermann, Paris, 1941–49).Google Scholar
5. Freiling, C. and Rinne, D., A symmetric density property: monotonicity and the approximate symmetric derivative (manuscript) 1988.Google Scholar
6. Henstock, R., Generalized integrals of vector-valued functions, Proc. London Math. Soc. (3) 19 (1969), 317–344.Google Scholar
7. James, R.D., A generalised integral (II), Canadian J. Math. 2 (1950), 297–306.Google Scholar
8. Kolmogorov, A., Üntersuchen tiber der integralbegriffe, Math. Annalen 103 (1930), 654–696.Google Scholar
9. Larson, L., The symmetric derivative, Trans. Amer. Math. Soc. 277 (1983), 589–599.Google Scholar
10. Leader, S., A concept of differential based on variational equivalence under generalized Riemann integration, Real Analysis Exchange 12 (1986), 144–175.Google Scholar
11. Leader, S., What is a differential? A new answer from the generalized Riemann integral, American Math. Monthly 93 (1986), 348–356.Google Scholar
12. Luxemburg, W.A.J. and Zaanen, A.C., Riesz spaces (North-Holland, Amsterdam, 1971).Google Scholar
13. Marcinkiewicz, J. and Zygmund, A., On the differentiability of functions and the summability of trigonometrical series, Fund. Math. 26 (1936), 1–43.Google Scholar
14. Matousek, J., Approximate symmetric derivatives and montonicity, Comment. Math. Univ. Carolinae 27 (1986), 83–86.Google Scholar
15. Pfeffer, W., A note on the generalized Riemann integral, Proc. Amer. Math. Soc. 103 (1988), 1161–1166.Google Scholar
16. Preiss, D., A note on symmetrically continuous functions, Časopis Pest. Mat. 96 (1971), 262–264.Google Scholar
17. Saks, S., Theory of the Integral, Monografie Matematyczne 7 (Warsaw, 1937).Google Scholar
18. Skvorcov, V.A., Concerning definitions of P2-and SCP'-integrals, Vestnik Moscov. Univ. Ser. I Mat. Meh. 21 (1966), 12–19.Google Scholar
19. The mutual relationship between the AP-integral of Taylor and the P2-integral of james, Mat. Sb. 170 (112) (1966), 380–393.Google Scholar
20. Taylor, S.J., An integral of Perron's type defined with the help of trigonometric series, Quart. J. Math. Oxford (2) 6 (1955), 255–274.Google Scholar
21. Thomson, B.S., Derivation bases on the real line. I, II, Real Analysis Exchange, 8 (1982-83), 67–207 and 278-142.Google Scholar
22. Uher, J., Symmetrically differentiable functions are differentiable almost everywhere, Real Analysis Exchange 8 (1982/83), 253–260.Google Scholar
23. Verblunsky, S., On the theory of trigonometrical series (VII), Fund. Math. 23 (1934), 192–236.Google Scholar
24. Zygmund, A., Trigonometrical series, (Cambridge University Press, London, 1968).Google Scholar