Hostname: page-component-7479d7b7d-fwgfc Total loading time: 0 Render date: 2024-07-12T02:30:08.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Anticommuting Linear Transformations

Published online by Cambridge University Press:  20 November 2018

H. Kestelman
H. Kestelman*
Affiliation:
University College, London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that any set of four anticommuting involutions (see §2) in a four-dimensional vector space can be represented by the Dirac matrices

(1)

where the B1,r are the Pauli matrices

(2)

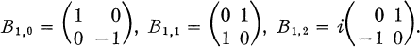
(See (1) for a general exposition with applications to Quantum Mechanics.) One formulation, which we shall call the Dirac-Pauli theorem (2; 3; 1), is

Theorem 1. If M1,M2, M3, M4 are 4 X 4 matrices satisfying

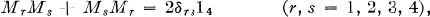
then there is a matrix T such that

and T is unique apart from an arbitrary numerical multiplier.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 614 - 624
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Good, R. H., Properties of the Dirac matrices, Rev. Mod. Phys., 27 (1955), 187.Google Scholar
2. Dirac, P. A. M., The quantum theory of the electron, Proc. Roy. Soc. A., 117 (1928), 616.Google Scholar
3. Pauli, W., Contributions mathématiques à la théorie de Dirac, Ann. Inst. Henri Poincaré, 6 (1936), 109.Google Scholar
4. Van der Waerden, B. L., Die Gruppentheoretische Méthode in der Quantenmechanik (Berlin, 1932) 55.Google Scholar
5. Eddington, A. S., On sets of anticommuiing matrices, J. London Math. Soc, 17 (1932), 58.Google Scholar
6. Newman, M. H. A., Note on an algebraic theorem of Eddington, J. London Math. Soc, 17 (1932), 93.Google Scholar
7. Hurwitz, A., Ueber die Komposition der Quadratischen Formen, Math. Annalen, 88 (1923), 1.Google Scholar