Article contents
Residual torsion-free nilpotence, bi-orderability, and two-bridge links
Published online by Cambridge University Press: 25 January 2023
Abstract
Residual torsion-free nilpotence has proved to be an important property for knot groups with applications to bi-orderability and ribbon concordance. Mayland proposed a strategy to show that a two-bridge knot group has a commutator subgroup which is a union of an ascending chain of para-free groups. This paper proves Mayland’s assertion and expands the result to the subgroups of two-bridge link groups that correspond to the kernels of maps to 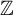 $\mathbb{Z}$. We call these kernels the Alexander subgroups of the links. As a result, we show the bi-orderability of a large family of two-bridge link groups. This proof makes use of a modified version of a graph-theoretic construction of Hirasawa and Murasugi in order to understand the structure of the Alexander subgroup for a two-bridge link group.
$\mathbb{Z}$. We call these kernels the Alexander subgroups of the links. As a result, we show the bi-orderability of a large family of two-bridge link groups. This proof makes use of a modified version of a graph-theoretic construction of Hirasawa and Murasugi in order to understand the structure of the Alexander subgroup for a two-bridge link group.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The work was supported by NSF grants DMS-1937215 and DMS-2213213.
References
- 1
- Cited by





