Research Article
Annihilator graphs and semigroups of matrices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
On generalised mixed co-quasi-variational inequalities with noncompact valued mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 7-15
-
- Article
-
- You have access
- Export citation
ABS-type methods for solving full row rank linear systems using a new rank two update
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 17-34
-
- Article
-
- You have access
- Export citation
The curvature and topological properties of hypersurfaces with constant scalar curvature
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 35-44
-
- Article
-
- You have access
- Export citation
On hypercyclicity and supercyclicity criteria
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-54
-
- Article
-
- You have access
- Export citation
A Riemannian invariant and its applications to Einstein manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-65
-
- Article
-
- You have access
- Export citation
Twisted Alexander polynomial for the Lawrence-Krammer representation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-71
-
- Article
-
- You have access
- Export citation
Pseudo-differential equations connected with p-adic forms and local zeta functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-86
-
- Article
-
- You have access
- Export citation
Characterisation of the sub-Riemannian isometry groups of the H-type groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 87-100
-
- Article
-
- You have access
- Export citation
Topological entropy for the canonical completely positive maps on graph C*-Algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-116
-
- Article
-
- You have access
- Export citation
Polynomials on banach spaces whose duals are isomorphic to ℓ1 (Γ)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-124
-
- Article
-
- You have access
- Export citation
Trace of Frobenius endomorphism of an elliptic curve with complex multiplication
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 125-142
-
- Article
-
- You have access
- Export citation
Classification theorems for the C*-Algebras of graphs with sinks
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 143-161
-
- Article
-
- You have access
- Export citation
On τ-completely decomposable modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-175
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 70 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 70 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

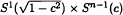 , where
, where 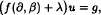 where
where 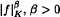 ,
, 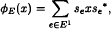 then Voiculescu's topological entropy ht(φ
then Voiculescu's topological entropy ht(φ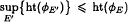 , where the supremum is taken over the set of all finite subgraphs of
, where the supremum is taken over the set of all finite subgraphs of