Research Article
On orders of directly indecomposable finite rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-359
-
- Article
-
- You have access
- Export citation
A note on analytic capacity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-365
-
- Article
-
- You have access
- Export citation
Stability of weak normal structure in James quasi reflexive space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-372
-
- Article
-
- You have access
- Export citation
Oscillations of certain partial differential equations with deviating arguments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 373-380
-
- Article
-
- You have access
- Export citation
On strongly right bounded finite rings II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 381-384
-
- Article
-
- You have access
- Export citation
On sufficiency of the Kuhn-Tucker conditions in nondifferentiable programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-389
-
- Article
-
- You have access
- Export citation
On the Schwarzian coefficients of univalent functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-400
-
- Article
-
- You have access
- Export citation
On the number of zeros of exponential polynomials and related questions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-412
-
- Article
-
- You have access
- Export citation
Ishikawa and Mann iteration methods for nonlinear strongly accretive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-424
-
- Article
-
- You have access
- Export citation
Some notes on the method of moving planes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-434
-
- Article
-
- You have access
- Export citation
On Gaussian elimination and determinant formulas for matrices with chordal inverses
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-440
-
- Article
-
- You have access
- Export citation
The stability of solutions in an initial-boundary reaction-diffusion system
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-448
-
- Article
-
- You have access
- Export citation
Local invertibility in subrings of C*(X)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-458
-
- Article
-
- You have access
- Export citation
Hecke groups and continued fractions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-474
-
- Article
-
- You have access
- Export citation
Finite Hilbert transforms and compactness
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-478
-
- Article
-
- You have access
- Export citation
The number of lattice rules having given invariants
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 479-495
-
- Article
-
- You have access
- Export citation
Characteristic subgroups of relatively free groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 497-507
-
- Article
-
- You have access
- Export citation
Topological and order-topological orthomodular lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 509-518
-
- Article
-
- You have access
- Export citation
Some nil ring properties related to T-nilpotence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 519-523
-
- Article
-
- You have access
- Export citation
An internal characterisation of strongly regular rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 525-528
-
- Article
-
- You have access
- Export citation

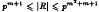 . As a consequence, we have that, for a given finite nilpotent ring
. As a consequence, we have that, for a given finite nilpotent ring 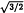 .
.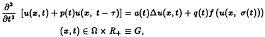
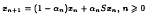
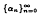 converges strongly to a solution of the equation
converges strongly to a solution of the equation 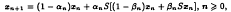
 and
and  converges strongly to a solution of the equation
converges strongly to a solution of the equation 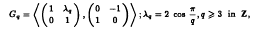
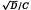 has nearly the form of the classical case. From this, we give: (1) a necessary and sufficient condition for
has nearly the form of the classical case. From this, we give: (1) a necessary and sufficient condition for 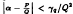 < γ
< γ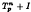 is not strictly singular whenever
is not strictly singular whenever  of an orthomodular lattice
of an orthomodular lattice