Research Article
On metric regularity of multifunctions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
The Attouch-Wets topology and a characterisation of normable linear spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 11-18
-
- Article
-
- You have access
- Export citation
Bounds on the fitting length of finite soluble groups with supersoluble Sylow normalisers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 19-31
-
- Article
-
- You have access
- Export citation
The patterns of the isonemal two-colour two-way two-fold fabrics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-43
-
- Article
-
- You have access
- Export citation
Commutativity conditions on rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-47
-
- Article
-
- You have access
- Export citation
Covariance function and ergodicity of asymptotically stationary random fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-62
-
- Article
-
- You have access
- Export citation
Commutativity of rings satisfying certain polynomial identities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-69
-
- Article
-
- You have access
- Export citation
On the l-adic representations attached to simple abelian varieties of type IV
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-78
-
- Article
-
- You have access
- Export citation
Positive solutions of a class of biological models in a heterogeneous environment
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-94
-
- Article
-
- You have access
- Export citation
Relative normal-convexity and amalgamations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 95-107
-
- Article
-
- You have access
- Export citation
Equivalence classes of inverse orthogonal and unit Hadamard matrices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-115
-
- Article
-
- You have access
- Export citation
On spectral decomposition of immersions of finite type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-129
-
- Article
-
- You have access
- Export citation
Representation of type A monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 131-138
-
- Article
-
- You have access
- Export citation
Perturbations of a Hamiltonian family of cubic vector fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 139-147
-
- Article
-
- You have access
- Export citation
An estimate of Ramanujan related to the greatest integer function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-154
-
- Article
-
- You have access
- Export citation
Fractions of the period of the continued fraction expansion of quadratic integers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-169
-
- Article
-
- You have access
- Export citation
Abstracts of Australian PhD Thesis
Study of a nonlinear control algorithm using dynamical systems theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 171-174
-
- Article
-
- You have access
- Export citation
Studies in radical theory for restricted classes of associative rings
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 175
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 44 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 44 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation

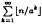 stated by Ramanujan in his notebooks.
stated by Ramanujan in his notebooks.