Research Article
Equivalent conditions of a tree map with zero topological entropy
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-327
-
- Article
-
- You have access
- Export citation
On the exponents modulo 3 in the standard factorisation of n!
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-334
-
- Article
-
- You have access
- Export citation
Linear structure of weighted holomorphic non-extendibility
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 335-344
-
- Article
-
- You have access
- Export citation
Existence of Torus bundles associated to cocycles
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-351
-
- Article
-
- You have access
- Export citation
Multiple solutions for some Neumann problems in exterior domains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-364
-
- Article
-
- You have access
- Export citation
Minimal surfaces in 3-dimensional solvable Lie groups II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-374
-
- Article
-
- You have access
- Export citation
Relative Abelian kernels of some classes of transformation monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-404
-
- Article
-
- You have access
- Export citation
Universality of methods approximating the derivative
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-411
-
- Article
-
- You have access
- Export citation
The Helgason Fourier transform for semisimple Lie groups I: The Case of SL2(ℝ)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-432
-
- Article
-
- You have access
- Export citation
Non-residues and primitive roots in Beatty sequences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-443
-
- Article
-
- You have access
- Export citation
The structure of reversing symmetry groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 445-459
-
- Article
-
- You have access
- Export citation
On the lengths of pairs of complex matrices of size at most five
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-472
-
- Article
-
- You have access
- Export citation
The Γ-opial property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-476
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Graphical trades
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-478
-
- Article
-
- You have access
- Export citation
Quantum superalgebras at roots of unity and topological invariants of three-manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 479
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 73 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 73 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

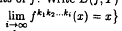 and g =
and g = 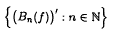 form a dense subset of
form a dense subset of 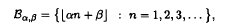 where α,β ∈ ℝ, and α is irrational. In particular, our bounds imply that for every fixed ε > 0, if
where α,β ∈ ℝ, and α is irrational. In particular, our bounds imply that for every fixed ε > 0, if