Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dragomir, Silvestru Sever
2016.
SOME TRACE INEQUALITIES FOR CONVEX FUNCTIONS OF SELFADJOINT OPERATORS IN HILBERT SPACES.
Korean Journal of Mathematics,
Vol. 24,
Issue. 2,
p.
273.
Dragomir, Sever S.
2016.
Reverse Jensen’s type Trace Inequalities for Convex Functions of Selfadjoint Operators in Hilbert Spaces.
Annales Mathematicae Silesianae,
Vol. 30,
Issue. 1,
p.
39.
Dragomir, S.S.
2016.
Some trace inequalities of Čebyšev type for functions of operators in hilbert spaces.
Linear and Multilinear Algebra,
Vol. 64,
Issue. 9,
p.
1800.
Dragomir, Sever S.
2017.
Trace inequalities of Cassels and Grüss type for operators in Hilbert spaces.
Acta Universitatis Sapientiae, Mathematica,
Vol. 9,
Issue. 1,
p.
74.
Taghavi, A.
Darvish, V.
Nazari, H. M.
and
Dragomir, S. S.
2017.
Some singular value and unitarily invariant norm inequalities for Hilbert space operators.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 63,
Issue. 2,
p.
377.
Dragomir, S. S.
2018.
Trace inequalities for positive operators via recent refinements and reverses of Young’s inequality.
Special Matrices,
Vol. 6,
Issue. 1,
p.
180.
Dragomir, S. S.
2018.
Some inequalities for trace class operators via a Kato’s result.
Asian-European Journal of Mathematics,
Vol. 11,
Issue. 01,
p.
1850004.
Dragomir, Silvestru Sever
2018.
Power and hölder type trace inequalities for positive operators in Hilbert spaces.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 55,
Issue. 3,
p.
383.
Kian, Mohsen
and
Alomari, Mohammad W.
2022.
Improvements of trace inequalities for convex functions.
Annals of Functional Analysis,
Vol. 13,
Issue. 4,
Aubeelack, Hema
Segonds, Stéphane
Bes, Christian
Druot, Thierry
Bérard, Adrien
Duffau, Marylène
and
Gallant, Guillaume
2022.
New Methodology for Robust-Optimal Design with Acceptable Risks: An Application to Blended/Wing/Body Aircraft.
AIAA Journal,
Vol. 60,
Issue. 5,
p.
3048.
Jones, Dalton
and
Dahleh, Munther A.
2022.
Closed Loop System Identification With Known Feedback: A Non Asymptotic Viewpoint.
p.
4094.
Liu, Xiang
Huang, Tianyao
and
Liu, Yimin
2022.
Transmit Design for Joint MIMO Radar and Multiuser Communications With Transmit Covariance Constraint.
IEEE Journal on Selected Areas in Communications,
Vol. 40,
Issue. 6,
p.
1932.
Guel-Cortez, Adrian-Josue
and
Kim, Eun-Jin
2023.
Relations between entropy rate, entropy production and information geometry in linear stochastic systems.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2023,
Issue. 3,
p.
033204.
Andrei, Vlad C.
Li, Xinyang
Mönich, Ullrich J.
and
Boche, Holger
2023.
Sensing-Assisted Receivers for Resilient-By-Design 6G MU-MIMO Uplink.
p.
1.
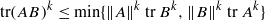 for any positive integer k.
for any positive integer k.



